题目内容
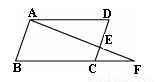
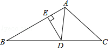
(本题10分)在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B作⊙O的切线BF交CD的延长线于点F,AC∥BF.


(1)如图1,求证:FG=FB;
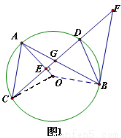
(2)如图2,连接BD、AC,若BD=BG,求证:AC∥BF;
(3)在(2)的条件下,若tan∠F=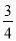 ,CD=1,求⊙O的半径
,CD=1,求⊙O的半径
(1)(2)证明见解析;(3)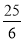
【解析】
试题分析:(1)连接OB,由BF是圆的切线可得直角,又有垂直,对顶角,利用等角的余角相等即可证;
(2)∠CAB和∠BDC都是弧BC所对的圆周角可证∠CAB=∠BDC,又可证∠DGB=∠GDB就可证∠CAB=∠GBF,即可证得平行;
(3)由平行可得∠ACE=∠F就得到tan∠F=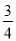 =tan∠ACE,由垂径定理可的CE=
=tan∠ACE,由垂径定理可的CE=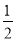 ,再由勾股定理求得AE,连接OE再用勾股定理求得半径.
,再由勾股定理求得AE,连接OE再用勾股定理求得半径.
试题解析:证明:(1)如图1
连接OB ∵BF是⊙O的切线
∴∠OBF=90°
∴∠OBA+∠GBF=90°
∵OA⊥CD
∴∠AEG=90° ∴∠AGE+∠EAG=90°
∵OA=OB
∴∠OAB=∠OBA
∴∠AGE=∠FBG
∵∠AGE=∠FGB
∴∠FGB=∠FBG
∴FG=FB
(2)∵BD=BG ∴∠DGB=∠GDB
∵∠CAB和∠BDC都是弧BC所对的圆周角
∴∠CAB=∠BDC
∴∠CAB=∠FGB
∵∠FGB=∠FBG
∴∠CAB=∠GBF
∴AC∥FB
【解析】
(3) 由(2)得∠FBG=∠CAG ∵∠FGB=∠FBG
∴∠CAG=∠FGB ∵∠FGB=∠CGA
∴∠CGA=∠CAG ∴CA=CG
∵AC∥BF∴∠ACE=∠F∴ tan∠ACE=tan∠F
∵tan∠F=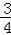 ∴tan∠ACE=
∴tan∠ACE=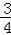 ∴
∴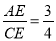
设AE=3k,则CE=4k. 在Rt△ACE中,
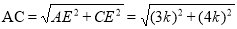 =5k
=5k
∴CG=5k
∴EG=CG-CE=5k-4k=k
∴k=1
∴CE=4,AE=3
连接OC,设⊙O的半径为R ,在Rt△CEO中,
CO2=CE2+OE 2 R2=42+(R-3) 2 解得R= 
即⊙O的半径为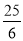 .
.
考点: 切线的性质定理,勾股定理,平行的判定.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
 中,
中, ,
, ,
, ,
, ,
, ,求四边形
,求四边形
 ,
, ,
,  ,
, ,3.14中,无理数有( )
,3.14中,无理数有( )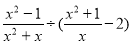 ,其中x=2cos30°+tan45.
,其中x=2cos30°+tan45.