题目内容
如图,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,CE⊥AE于E,BD⊥AE于D,DE=4cm,CE=2cm,则BD= 。
6cm.
【解析】
试题分析:利用同角的余角相等求出∠ABD=∠CAE,再利用“角角边”证明△ABD和△CAE全等,根据全等三角形对应边相等可得BD=AE,AD=CE,然后计算即可得解.
试题解析:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥AE,
∴∠ABD+∠BAD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE=CE+DE=2+4=6cm,
∴BD=6cm.
考点:全等三角形的判定与性质.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目


 ,②
,② ,③
,③ ,④
,④ 中分式有( )个.
中分式有( )个.

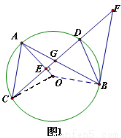


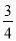 ,CD=1,求⊙O的半径
,CD=1,求⊙O的半径