��Ŀ����
14���Ķ�����IJ������ɶ������ض��������֤�����ֶ����������ǽ̲��н��ܵ�һ��ƴͼ֤�����ɶ����ķ����������ĸ�ȫ�ȵ�ֱ�������Σ������ǵ�����ֱ�DZ߷ֱ�Ϊa��b��б��Ϊc��Ȼ��ͼ1�ķ��������ǰڳ������Σ�
��ͼ1���Եõ���a+b��2=4��$\frac{1}{2}$ab+c2
��������a2+2ab+b2=2ab+c2��
����a2+b2=c2��
�����ͼ1�е��ĸ�ȫ�ȵ�ֱ�������ΰڳ�ͼ2��ʾ�������Σ����������������֤�����ɶ�����
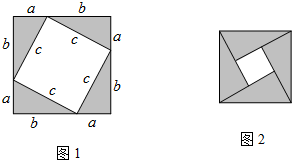
���� ֱ������ͼ������ó���ʽ�����������ó��𰸣�
���  ֤������S��������=c2��S��������=4S��+SС������=4��$\frac{1}{2}$ab+��b-a��2��
֤������S��������=c2��S��������=4S��+SС������=4��$\frac{1}{2}$ab+��b-a��2��
��c2=4��$\frac{1}{2}$ab+��b-a��2��
��������2ab+b2-2ab+a2=c2��
��c2=a2+b2��
���� ������Ҫ�����˹��ɶ�����֤������ȷ��ʾ��ͼ������ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
9�����и����У���������ĸ��������ǣ�������
| A�� | $\frac{1}{3x}$��$\frac{a}{6{x}^{2}}$���ĸ��6x2 | |
| B�� | $\frac{1}{m+n}$��$\frac{1}{m-n}$�����ĸ�ǣ�m+n����m-n�� | |
| C�� | $\frac{1}{3{a}^{2}{b}^{3}}$��$\frac{1}{3{a}^{2}{b}^{3}c}$���ĸ��3a2b3c | |
| D�� | $\frac{1}{a��x-y��}$��$\frac{1}{b��y-x��}$�����ĸ��ab��x-y����y-x�� |
19��������3����С��ͬ��С������2��Ϊ��ɫ��1��Ϊ��ɫ��ÿ�δӴ�����1����Ȼ��Żؽ���������������ʵ���еõ��±��в������ݣ�
��1���뽫���ݱ�����������
��2��������������Ƶ�ʵ�����ͳ��ͼ��
��3������һ������ĸ��ʹ���ֵ�Ƕ��٣�
| ������� | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| ���ֺ�ɫ��Ƶ�� | 14 | 24 | 38 | 68 | 77 | 92 | 109 | 120 | 132 | |
| �����ɫ��Ƶ�� | 35% | 32% | 35% | 34% | 33% | 34% |
��2��������������Ƶ�ʵ�����ͳ��ͼ��
��3������һ������ĸ��ʹ���ֵ�Ƕ��٣�
6�����㣨-2��y1������-1��y2������1��y3���ڷ���������y=$\frac{2}{x}$��ͼ���ϣ������н����У���ȷ���ǣ�������
| A�� | y1��y2��y3 | B�� | y2��y1��y3 | C�� | y3��y1��y2 | D�� | y3��y2��y1 |
4��ij�����ε����Ϊ9x2y-6xy2������һ�߳�Ϊ3xy������һ�߳�Ϊ��������
| A�� | 3x-2y | B�� | 9x-6y | C�� | 3x-2 | D�� | 6x-4y |
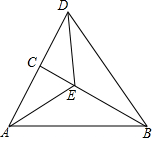 ��ͼ����֪�ڡ�ABC�У���ACB=90�㣬��BAC=60�㣬AE�ǡ�BAC��ƽ���ߣ��ӳ�AC����D��ʹCD=AC��
��ͼ����֪�ڡ�ABC�У���ACB=90�㣬��BAC=60�㣬AE�ǡ�BAC��ƽ���ߣ��ӳ�AC����D��ʹCD=AC��
 ��һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���C����ͼ��ʾ�ķ�ʽ������һ��
��һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���C����ͼ��ʾ�ķ�ʽ������һ��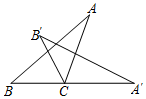 ��ͼ������ABC�Ƶ�C��˳ʱ�뷽����ת64������A��B��C��ʹ��A������BC���ӳ����ϣ����ACB��=52�ȣ�
��ͼ������ABC�Ƶ�C��˳ʱ�뷽����ת64������A��B��C��ʹ��A������BC���ӳ����ϣ����ACB��=52�ȣ�