题目内容
9．若关于x的一元二次方程x2+2（m-2）x+m2=0没有实数根，则m的取值范围是（ ）| A． | m＞1 | B． | m≥1 | C． | m＜1 | D． | m≤1 |
分析 根据方程没有实数根可知△＜0，求出m的取值范围即可．
解答 解：∵关于x的一元二次方程x2+2（m-2）x+m2=0没有实数根，
∴△＜0，即△=4（m-2）2-4m2＜0，解得m＞1．
故选A．
点评 本题考查的是根的判别式，熟知一元二次方程的根与△=b2-4ac的关系是解答此题的关键．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图，直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（-1，m）．
如图，在?ABCD中，E，F分别在AD，BC上，且AE=CF，连结BE、DF．
14．绝对值是$\sqrt{5}$的实数是（ ）
| A． | ±$\sqrt{5}$ | B． | $\sqrt{5}$ | C． | -$\sqrt{5}$ | D． | ±5 |
1．
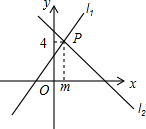如图l1：y=x+3与l2：y=ax+b相交于点P（m，4），则关于x的不等式x+3≤ax+b的解为（ ）
如图l1：y=x+3与l2：y=ax+b相交于点P（m，4），则关于x的不等式x+3≤ax+b的解为（ ）| A． | x≥4 | B． | x＜m | C． | x≥m | D． | x≤1 |