Question

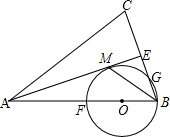已知：如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．
（1）求证：AE与⊙O相切；
（2）若BC=6，AB=AC=10，求⊙O的半径．

Answer 1

考点：切线的判定

专题：

分析：（1）连接OM，可得∠OMB=∠OBM=∠MBE，根据∠OMB+∠BME=∠MBE+∠BME=90°即可证明；
（2）由△AOM∽△ABE，根据相似三角形对应边成比例即可求解．

解答：（1）证明：连接OM，
则∠OMB=∠OBM=∠MBE
又∵AB=AC，AE是角平分线，
∴AE⊥BC，
∴∠OMB+∠BME=∠MBE+∠BME=90°，∴∠AMO=90°，
∴AE与⊙O相切．

（2）解：由AE与⊙O相切，AE⊥BC
∴OM∥BC
∴△AOM∽△ABE
∴

OM

BE

=

AO

AB

，
∵BC=6
∴BE=3，AB=10，
即

r

3

=

10-r

10

，
解得：r=

30

13

．

点评：本题考查了相似三角形的判定与性质，属于基础题，关键是作出辅助线进行证明．