题目内容
 如图,直线l与⊙O相切于点M,点P为直线l上一点,直线PO交⊙O于点A、B,点C在线段PM上,连接BC,且CM=BC.
如图,直线l与⊙O相切于点M,点P为直线l上一点,直线PO交⊙O于点A、B,点C在线段PM上,连接BC,且CM=BC.(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AB=2BP,⊙O的半径为6cm,求图中阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)首先证明△OBC≌△OMC(SSS),得出∠CBO=∠CMO=90°,即可得出直线BC是⊙O的切线;
(2)利用切线的性质定理以及勾股定理和锐角三角函数关系得出∠POM=60°,则∠MOA=120°,以及AM的长,再利用三角形面积公式以及扇形面积公式得出答案即可.
(2)利用切线的性质定理以及勾股定理和锐角三角函数关系得出∠POM=60°,则∠MOA=120°,以及AM的长,再利用三角形面积公式以及扇形面积公式得出答案即可.
解答:解:(1)直线BC是⊙O的切线,
理由:连接MO,CO,
∵直线l与⊙O相切于点M,
∴∠PMO=90°,
在△OBC和△OMC中
,
∴△OBC≌△OMC(SSS),
∴∠CBO=∠CMO=90°,
∴直线BC是⊙O的切线;
 (2)过点O作ON⊥AM于点N,
(2)过点O作ON⊥AM于点N,
∵AB=2BP,
∴PB=BO=MO,
即MO=
PO,
又∵∠PMO=90°,
∴∠MPO=30°,
∴∠POM=60°,则∠MOA=120°,
∴S扇形AOM=
=12π(cm2),
∵∠MOA=120°,ON⊥AM,
∴∠MON=∠AON=60°,
∴NO=
×6=3(cm),
MN=CO•sin60°=
×6=3
(cm),
∴AM=6
cm,则S△AOM=
×NO×AM=
×3×6
=9
(cm2),
∴图中阴影部分的面积为:(12π-9
)cm2.
理由:连接MO,CO,
∵直线l与⊙O相切于点M,
∴∠PMO=90°,
在△OBC和△OMC中
|
∴△OBC≌△OMC(SSS),
∴∠CBO=∠CMO=90°,
∴直线BC是⊙O的切线;
 (2)过点O作ON⊥AM于点N,
(2)过点O作ON⊥AM于点N,∵AB=2BP,
∴PB=BO=MO,
即MO=
| 1 |
| 2 |
又∵∠PMO=90°,
∴∠MPO=30°,
∴∠POM=60°,则∠MOA=120°,
∴S扇形AOM=
| 120π×62 |
| 360 |
∵∠MOA=120°,ON⊥AM,
∴∠MON=∠AON=60°,
∴NO=
| 1 |
| 2 |
MN=CO•sin60°=
| ||
| 2 |
| 3 |
∴AM=6
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
9
| ||
| 4 |
∴图中阴影部分的面积为:(12π-9
| 3 |
点评:此题主要考查了扇形面积公式以及切线的性质和判定和锐角三角函数关系应用和勾股定理等知识,熟练应用切线的性质和判定定理是解题关键.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列函数中,自变量x可以取1和2的函数是( )
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
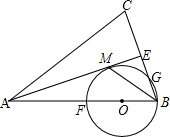 已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径. 解不等式组
解不等式组