题目内容
4.如图(1),⊙O的半径为1cm,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M在CD的延长线上,AM所在的直线交于⊙O于点N,点P在线段DM上,且PN与⊙O相切于点N.(1)求证:PM=PN;
(2)连结AC、CN,如图(2),若∠AMO=30°,求图中阴影部分的面积.

分析 (1)连结ON,根据同圆的半径相等,得到OA=ON,∠ONA=∠OAN,由等腰三角形的判定与性质定理推出结论.
(2)连结ON,作NE⊥OD,由含30°的直角三角形的性质得到NE=$\frac{1}{2}ON=\frac{1}{2}$,根据扇形的面积公式求出结果.
解答  (1)证明:连结ON,
(1)证明:连结ON,
∵OA=ON,∴∠ONA=∠OAN,
在Rt△AOM中,
∵∠PMN+∠OAM=90°,
∴∠PMN+∠ONA=90°,
∵PN与⊙O相切,
∴∠PNO=90°,∴∠PNM+∠ONA=90°,
∴∠PNM=∠PMN,
∴PM=PN.
(2)解:连结ON,作NE⊥OD,垂足为点E,
∵∠AMO=30°,PM=PN,
∴∠PNM=30°,∠OPN=60°,
∵∠ONP=90°,∴∠PON=30°,
则NE=$\frac{1}{2}ON=\frac{1}{2}$,
∵∠AOM=90°,∴∠AON=60°.
∴S阴影=S△AOC+S扇形AON-S△CON=$\frac{1}{2}×1×1+\frac{60}{360}π×1-\frac{1}{2}×1×\frac{1}{2}$=$\frac{1}{4}+\frac{π}{6}$.
点评 本题考查了切线的性质,等腰三角形的判定与性质,含30°的直角三角形的性质,扇形的面积公式,作出正确的辅助线是解题的关键.

练习册系列答案
相关题目
19.如图,搭第一个图形需要7根火柴棒.
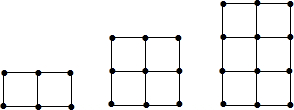
(1)搭一搭,填一填:
(2)搭n个图形需要5n+2根火柴棒.

(1)搭一搭,填一填:
| 第几个图形 | 1 | 2 | 3 | 4 | … |
| 火柴棒根数 | 7 | 12 | 17 | 22 | … |
13.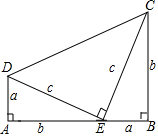 用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
 用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)(a+b)=a2-b2 | C. | a2+b2=c2 | D. | c2-a2=(c-a)(c+a) |
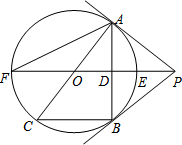 如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.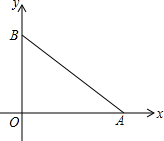 在平面直角坐标系中,已经A(8,0),B(0,6)
在平面直角坐标系中,已经A(8,0),B(0,6) 如图,若∠BAC=∠DCA,则可以判定图中互相平行的线段是AB∥CD.
如图,若∠BAC=∠DCA,则可以判定图中互相平行的线段是AB∥CD.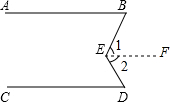 完成正确的证明如图,已知AB∥CD,求证:∠BED=∠B+∠D
完成正确的证明如图,已知AB∥CD,求证:∠BED=∠B+∠D