题目内容
13.探究:在矩形ABCD中,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
(1)如图1,求证:ME=MF;
(2)如图2,点G是线段BC上一点,连接GE、GF、GM,若△EGF是等腰直角三角形,∠EGF=90°,求AB:AB的值;
(3)如图3,点G是线段BC延长线上一点,连接GE、GF、GM,若△EGF是等边三角形,直接写出AB、AD满足的数量关系.
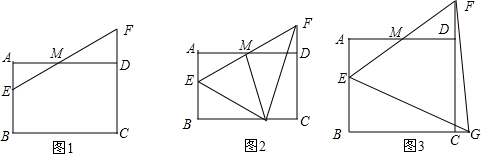
分析 (1)根据ABCD是矩形,得出∠EAM=∠FDM=90°,根据AM=DM,∠AME=∠FMD证出△AEM≌△DFM,即可得出ME=FM;
(2)过点G作GH⊥AD于H,则AB=GH,根据△GEF是等腰直角三角形,得出ME=FM,GM⊥EF,根据∠MGE=∠MGF=45°,∠AME+∠GMH=90°,得出∠MGE=∠MEG=45°,ME=MG,再根据∠AME+∠AEM=90°,得出∠AEM=∠GMH从而证出△AEM≌△HMG,得出GH=AM,即可解答;
(3)过点G作GH⊥AD交AD延长线于点H,连接MG,则∠GHM=∠A,根据△GEF是等边三角形,得出EM=FM,GM⊥EF,$\frac{EM}{GM}=cot6{0}^{°}=\frac{\sqrt{3}}{3}$,∠AME+∠GMH=90°,根据∠AME+∠AEM=90°,得出∠GMH=∠AEM,证出△AEM∽△HMG,$\frac{AM}{HG}=\frac{EM}{GM}=\frac{\sqrt{3}}{3}$,得出HG=$\sqrt{3}$AM,最后根据AB=HG即可求出答案.
解答 (1)证明:如图1,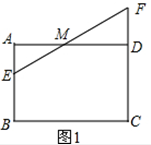
在矩形ABCD中,
∠A=∠FDM=90°.
又∵AM=DM,∠AME=∠DMF,
∴△AME≌△DMF.
∴ME=MF.
(2)解:如图2,过点G作GH⊥AD于点H.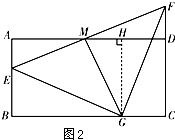
∴四边形ABGH是矩形.
∵△EGF是等腰直角三角形,
由(1)得,ME=MF,
∴ME=MG,
∠EMG=90°.
∴∠AME+∠DMG=∠HGM+∠DMG=90°.
∴∠AME=∠HGM.
又∵∠A=∠MHG,
∴△AME≌△HGM,
∴AM=HG.
∴AB=HG=AM=$\frac{1}{2}$AD,
∴AD=2AB,
∴AB:AD=2:1,
(3)AB=$\frac{{\sqrt{3}}}{2}AD$,
如图3,过点G作GH⊥AD交AD延长线于点H,连接MG,则∠GHM=∠A,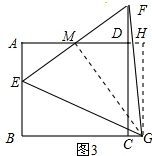
∵△GEF是等边三角形,EM=FM,
∴GM⊥EF,
∴$\frac{EM}{GM}=cot6{0}^{°}=\frac{\sqrt{3}}{3}$,
∠AME+∠GMH=90°,
∵∠AME+∠AEM=90°,
∴∠GMH=∠AEM,
∴△AEM∽△HMG,
∴$\frac{AM}{HG}=\frac{EM}{GM}=\frac{\sqrt{3}}{3}$,
∴HG=$\sqrt{3}$AM=$\sqrt{3}×\frac{AD}{2}=\frac{\sqrt{3}}{2}AD$,
∴AB=$\frac{\sqrt{3}}{2}AD$.
点评 此题考查了四边形综合,用到的知识点是全等三角形的判定及性质,相似三角形的判定及性质,三角函数值的运用,等边三角形、等腰直角三角形的性质.在解答时添加辅助线构建全等形和相似形是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案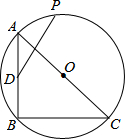 如图,等腰Rt△ABC内接于⊙O,AB=4$\sqrt{2}$,D为AB的中点,P为⊙O上一动点,则线段DP的最大值为4+2$\sqrt{2}$.
如图,等腰Rt△ABC内接于⊙O,AB=4$\sqrt{2}$,D为AB的中点,P为⊙O上一动点,则线段DP的最大值为4+2$\sqrt{2}$.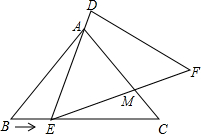 如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动(E不与B、C重合),且DE始终经过点A,EF与AC交于M点.
如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动(E不与B、C重合),且DE始终经过点A,EF与AC交于M点.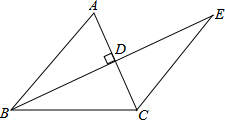 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=56°,求∠E的度数.
如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=56°,求∠E的度数.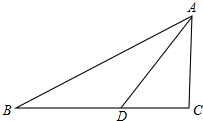 在Rt△ABC中,∠C=90°,tanB=$\frac{3}{4}$,∠ADC=45°,DC=6,求BD的长.
在Rt△ABC中,∠C=90°,tanB=$\frac{3}{4}$,∠ADC=45°,DC=6,求BD的长. 如图,这是我军缴获的敌人埋设地雷的地图.通过破译的密码知道,一棵大树作为参照物,树的坐标是(10,-10).这个区域埋设地雷的坐标分别是(10,20),(0,50),(-50,-40),(-40,40),(50,-30),(-10,0).
如图,这是我军缴获的敌人埋设地雷的地图.通过破译的密码知道,一棵大树作为参照物,树的坐标是(10,-10).这个区域埋设地雷的坐标分别是(10,20),(0,50),(-50,-40),(-40,40),(50,-30),(-10,0).