题目内容
1.求下列函数图象的对称轴、顶点坐标及开口方向:(1)y=-x2-2x:
(2)y=-$\frac{1}{2}$x2-x+2:
分析 先根据二次项系数确定开口方向,再将一般式化为顶点式即可确定顶点坐标和对称轴.
解答 解:(1)∵y=-x2-2x的二次项系数为-1,
∴开口方向向下;
∵y=-x2-2x=-(x+1)2+1,
∴顶点坐标为(-1,1),对称轴为x=-1;
(2)∵y=-$\frac{1}{2}$x2-x+2的二次项系数为-$\frac{1}{2}$,
∴开口方向向下;
∵y=-$\frac{1}{2}$x2-x+2=-$\frac{1}{2}$(x+1)2+$\frac{5}{2}$,
∴顶点坐标为(-1,$\frac{5}{2}$),对称轴为x=-1.
点评 本题考查了抛物线的开口方向,顶点坐标及对称轴与抛物线解析式的关系,关键是利用配方法将一般式化为顶点式.

练习册系列答案
相关题目
12.当x<0时,分式$\frac{|x|}{x}$的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 不确定 |
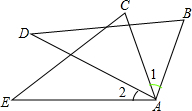 如图,已知AB=AC,∠B=∠C,且∠1=∠2.求证:△ABD≌△ACE.
如图,已知AB=AC,∠B=∠C,且∠1=∠2.求证:△ABD≌△ACE.