题目内容
如图，正三角形△A1B1C1的边长为1，取△A1B1C1各边的中点A2、B2、C2，作第二个正三角形△A2B2C2，再取△A2B2C2各边的中点A3、B3、C3，作第三个正三角形△A3B3C3，…用同样的方法作正三角形则第10个正三角形△A10B10C10的面积是 ．
【答案】分析：先求前几个三角形的面积，找出其中的规律，再求解．
解答：解：第一个三角形的面积S=
，
第二个三角形的面积S=
×
，
第三个三角形的面积S=
×（
）2，
…
所以第十个三角形的面积S=
×（
）9=
．
故答案为：
•
．
点评：熟练掌握等边三角形的性质，会求解等边三角形的面积问题．
解答：解：第一个三角形的面积S=
，第二个三角形的面积S=
×，第三个三角形的面积S=
×（）2，…
所以第十个三角形的面积S=
×（）9=．故答案为：
•．点评：熟练掌握等边三角形的性质，会求解等边三角形的面积问题．
练习册系列答案
相关题目
如图，正三角形A1OB1，正三角形A2B1B2，正三角形A3B2B3…按如图所示的方式放置．点A1，A2，A3，…和点B1，B2，B3…分别在直线
（2013•湛江）如图，所有正三角形的一边平行于x轴，一顶点在y轴上．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1、A2、A3、A4…表示，其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位，则顶点A3的坐标是
如图，在平面直角坐标系中，一个质点从原点O出发，每次都沿着与x轴成60°角的方向运动一个长度单位，依次向右上、右下、右上、右下…方向移动到A1、A2、A3、A4…，即△OA1A2、△A2A3A4、△A4A5A6…均为正三角形，则：
如图，正三角形A1OB1，正三角形A2B1B2，正三角形A3B2B3…按如图所示的方式放置．点A1，A2，A3，…和点B1，B2，B3…分别在直线
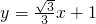和x轴上．那么点An的纵坐标是________．
和x轴上．那么点An的纵坐标是 ．