题目内容
 如图,正三角形A1OB1,正三角形A2B1B2,正三角形A3B2B3…按如图所示的方式放置.点A1,A2,A3,…和点B1,B2,B3…分别在直线y=
如图,正三角形A1OB1,正三角形A2B1B2,正三角形A3B2B3…按如图所示的方式放置.点A1,A2,A3,…和点B1,B2,B3…分别在直线y=
| ||
| 3 |
分析:设B1点坐标为(X1,0),根据题中关系可以得出A1点的坐标,同理根据Bn的坐标找到对应的An的坐标.
解答:解:设B1点坐标为(X1,0)
∵△A1OB1为正三角形.
∴A1的横坐标为
x1
∵A1在y=
x+1上
A1点坐标为(
x1,
x1)
∴代入方程得A1坐标(
,
);
设B1B2长度为x则A2坐标为(
+
,
x)
∴代入方程得x=
∴A2坐标(2
,3);
同理得A3坐标(5
,6);
由A1纵坐标
=
×21-1;
A2纵坐标3=
×22-1;
A3纵坐标6=
×23-1;
依此类推得An纵坐标为Yn=
×2n-1.
∵△A1OB1为正三角形.
∴A1的横坐标为
| 1 |
| 2 |
∵A1在y=
| ||
| 3 |
A1点坐标为(
| 1 |
| 2 |
| ||
| 2 |
∴代入方程得A1坐标(
| ||
| 2 |
| 3 |
| 2 |
设B1B2长度为x则A2坐标为(
| ||
| 2 |
| x |
| 2 |
| ||
| 2 |
∴代入方程得x=
3
| ||
| 2 |
∴A2坐标(2
| 3 |
同理得A3坐标(5
| 3 |
由A1纵坐标
| 3 |
| 2 |
| 3 |
| 2 |
A2纵坐标3=
| 3 |
| 2 |
A3纵坐标6=
| 3 |
| 2 |
依此类推得An纵坐标为Yn=
| 3 |
| 2 |
点评:本题重点在于结合三角函数和直线方程得出A1A2A3…的纵坐标,然后总结规律得到An的纵坐标.

练习册系列答案
相关题目
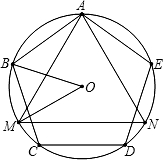 如图,正三角形AMN与正五边形ABCDE内接于⊙O,则∠BOM的度数是
如图,正三角形AMN与正五边形ABCDE内接于⊙O,则∠BOM的度数是
 如图,正三角形A1OB1,正三角形A2B1B2,正三角形A3B2B3…按如图所示的方式放置.点A1,A2,A3,…和点B1,B2,B3…分别在直线
如图,正三角形A1OB1,正三角形A2B1B2,正三角形A3B2B3…按如图所示的方式放置.点A1,A2,A3,…和点B1,B2,B3…分别在直线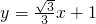 和x轴上.那么点An的纵坐标是________.
和x轴上.那么点An的纵坐标是________. 和x轴上.那么点An的纵坐标是 .
和x轴上.那么点An的纵坐标是 .