题目内容
20. 如图,△ABC中,∠ACB=135°,AC=4,在同一平面内,将△ABC绕点C顺时针方向旋转到△A′B′C,使得AA′∥CB,则AA′的长度为4$\sqrt{2}$.
如图,△ABC中,∠ACB=135°,AC=4,在同一平面内,将△ABC绕点C顺时针方向旋转到△A′B′C,使得AA′∥CB,则AA′的长度为4$\sqrt{2}$.
分析 根据平行线的性质求出∠A′AC,根据旋转的性质得出A′C=AC=4,求出∠A′AC=∠AA′C=45°,∠A′CA=90°,根据勾股定理求出即可.
解答 解:∵∠ACB=135°,AA′∥CB,
∴∠A′AC=180∠ACB=45°,
∵将△ABC绕点C顺时针方向旋转到△A′B′C,AC=4,
∴A′C=AC=4,
∴∠A′AC=∠AA′C=45°,
∴∠A′CA=90°,
由勾股定理得:AA′=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
故答案为:4$\sqrt{2}$.
点评 本题考查了旋转的性质,勾股定理,平行线的性质,能求出∠A′CA=90°是解此题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
10.自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化.小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格.(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣.
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费5元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交费1元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里.已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元.请问小林乘坐地铁和公交车的里程分别是多少公里?

| 
| ||||||||||||||||||||||||||||||
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣.
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费5元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交费1元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里.已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元.请问小林乘坐地铁和公交车的里程分别是多少公里?
11.甲、乙、丙3人聚会,每人带了一件礼物,将这3件礼物分别放在3个完全相同的盒子里,每人随机抽取一个礼盒(装有礼物的盒子)
(1)下列事件是必然事件的是C
(2)甲、乙、丙3人抽到的都不是自己带来的礼物(记为事件A),请列出事件A的所有可能的结果,并求事件A的概率.
(1)下列事件是必然事件的是C
| A 乙没有抽到自己带来的礼物 | B 乙恰好抽到自己带来的礼物 |
| C 乙抽到一件礼物 | D 只有乙抽到自己带来的礼物 |
5. 如图,△ABC中,BC=4,DE是中位线,则DE的长为( )
如图,△ABC中,BC=4,DE是中位线,则DE的长为( )
 如图,△ABC中,BC=4,DE是中位线,则DE的长为( )
如图,△ABC中,BC=4,DE是中位线,则DE的长为( )| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 2 |
12. 如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
 如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )
如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )| A. | 8 | B. | 4$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 8$\sqrt{2}$ |
9.若把一次函数y=2x-3,向下平移3个单位长度,得到图象解析式是( )
| A. | y=2x | B. | y=2x-6 | C. | y=5x-3 | D. | y=-x-3 |
 如图,反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象与一次函数y=k2x+b的图象交于A(1,6),B(m,2)两点.
如图,反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象与一次函数y=k2x+b的图象交于A(1,6),B(m,2)两点.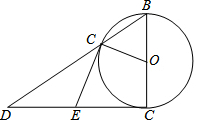 如图,⊙O的直径AB=4,点C为⊙O上的一个动点,连接OC,过点A作⊙O的切线,与BC的延长线交于点D,点E为AD的中点,连接CE.
如图,⊙O的直径AB=4,点C为⊙O上的一个动点,连接OC,过点A作⊙O的切线,与BC的延长线交于点D,点E为AD的中点,连接CE.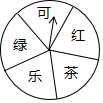 某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶、红茶和可乐.
某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶、红茶和可乐.