题目内容
 如图,五边形ABCDE中,P为BC上一点,∠PAE=∠APE,∠DAE=∠ADE,且EA⊥BA,PE⊥BC,ED⊥CD,若∠PDA=x°,∠PAD=y°,则∠C的度数为( )
如图,五边形ABCDE中,P为BC上一点,∠PAE=∠APE,∠DAE=∠ADE,且EA⊥BA,PE⊥BC,ED⊥CD,若∠PDA=x°,∠PAD=y°,则∠C的度数为( )| A、180°-2x° |
| B、180°-2y° |
| C、180°-x°-y° |
| D、90°+x°+y° |
考点:多边形内角与外角,等腰三角形的性质
专题:计算题
分析:根据等腰三角形的判定,由∠PAE=∠APE,∠DAE=∠ADE得到EA=EP,EP=ED,则点A、P、D在以E为圆心、EA为半径的圆上,根据圆周角定理得到∠PED=2∠PAD=2y°,然后根据四边形内角和定理得到∠C+∠EPC+∠EDC+∠PED=360°,所以∠C=180°-2y°.
解答:解:∵∠PAE=∠APE,∠DAE=∠ADE,
∴EA=EP,EP=ED,
∴EA=EP=ED,
∴点A、P、D在以E为圆心、EA为半径的圆上,
∴∠PED=2∠PAD=2y°,
∵PE⊥BC,ED⊥CD,
∴∠EPC=∠EDC=90°,
∵∠C+∠EPC+∠EDC+∠PED=360°,
∴∠C=180°-2y°.
故选B.
∴EA=EP,EP=ED,
∴EA=EP=ED,
∴点A、P、D在以E为圆心、EA为半径的圆上,
∴∠PED=2∠PAD=2y°,
∵PE⊥BC,ED⊥CD,
∴∠EPC=∠EDC=90°,
∵∠C+∠EPC+∠EDC+∠PED=360°,
∴∠C=180°-2y°.
故选B.
点评:本题考查了多边形的内角和外角:多边形内角和定理:(n-2).•80 (n≥3)且n为整数);多边形的外角和等于360度.也考查了等腰三角形的判定和圆周角定理.

练习册系列答案
相关题目
 已知二次函数y=-
已知二次函数y=- 如图,在矩形ABCD中,AD=2AB=2,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,那么AM=
如图,在矩形ABCD中,AD=2AB=2,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,那么AM=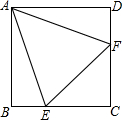 如图,点E、F分别是正方形ABCD边AB、CD上的两点,△CEF是边长为4的等边三角形,则正方形的边长是
如图,点E、F分别是正方形ABCD边AB、CD上的两点,△CEF是边长为4的等边三角形,则正方形的边长是