题目内容
抛物线y=-2x2+4x-1的开口方向是 ，对称轴是 ，顶点是 ．
考点：二次函数的性质
专题：
分析：用配方法把二次函数解析式转化为顶点式，可确定开口方向，对称轴及顶点坐标．
解答：解：∵y=-2x2+4x-1=-2（x-1）2+1，
∴二次项系数a=-2＜0，抛物线开口向下，
顶点坐标为（1，1），对称轴为直线x=1．
故答案为：下，x=1，（1，1）．
∴二次项系数a=-2＜0，抛物线开口向下，
顶点坐标为（1，1），对称轴为直线x=1．
故答案为：下，x=1，（1，1）．
点评：本题考查了二次函数的解析式与图象的开口方向，对称轴及顶点坐标的联系，关键是将一般式转化为顶点式．
练习册系列答案
小学课时特训系列答案
相关题目
若|x-3|+（y+3）2=0，则yx=（ ）
| A、-9 | B、9 | C、-27 | D、27 |
如图，五边形ABCDE中，P为BC上一点，∠PAE=∠APE，∠DAE=∠ADE，且EA⊥BA，PE⊥BC，ED⊥CD，若∠PDA=x°，∠PAD=y°，则∠C的度数为（ ）| A、180°-2x° |
| B、180°-2y° |
| C、180°-x°-y° |
| D、90°+x°+y° |
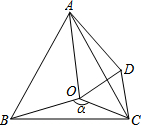如图，已知点O是等边AO=AD内一点，∠BOC=α，且OC=3．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD，则OD=
已知抛物线y=ax2+bx+c经过A（-1，0）、B（2，0）、C（0，2）三点．方程2x2+3x=0解是（ ）
| A、x1=0，x2=-3 | ||
B、x1=0，x2=
| ||
C、x1=0，x2=-
| ||
D、x1=0，x2=-
|