题目内容
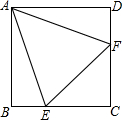 如图,点E、F分别是正方形ABCD边AB、CD上的两点,△CEF是边长为4的等边三角形,则正方形的边长是
如图,点E、F分别是正方形ABCD边AB、CD上的两点,△CEF是边长为4的等边三角形,则正方形的边长是考点:正方形的性质,等边三角形的性质,勾股定理
专题:
分析:根据正方形的性质可得AB=AD,∠B=∠D=90°,根据等边三角形的性质可得AE=AF,然后利用“HL”证明Rt△ABE和Rt△ADF全等,根据全等三角形对应边相等可得BE=DF,然后求出CE=CF,再根据等腰直角三角形的性质求出CE,设正方形的边长为x,表示出BE,然后利用勾股定理列方程求解即可.
解答:解:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
∵△CEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴BC-BE=CD-DF,
即CE=CF,
∴△CEF是等腰直角三角形,
∴CE=
×4=2
,
设正方形的边长为x,则BE=x-2
,
在Rt△ABE中,AB2+BE2=AE2,
即x2+(x-2
)2=42,
整理得,x2-2
x-4=0,
解得x1=
+
,x2=
-
(舍去),
所以,正方形的边长为
+
.
故答案为:
+
.
∴AB=AD,∠B=∠D=90°,
∵△CEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
|
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴BC-BE=CD-DF,
即CE=CF,
∴△CEF是等腰直角三角形,
∴CE=
| ||
| 2 |
| 2 |
设正方形的边长为x,则BE=x-2
| 2 |
在Rt△ABE中,AB2+BE2=AE2,
即x2+(x-2
| 2 |
整理得,x2-2
| 2 |
解得x1=
| 2 |
| 6 |
| 2 |
| 6 |
所以,正方形的边长为
| 2 |
| 6 |
故答案为:
| 2 |
| 6 |
点评:本题考查了正方形的性质,等边三角形的性质,全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,熟记各性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,五边形ABCDE中,P为BC上一点,∠PAE=∠APE,∠DAE=∠ADE,且EA⊥BA,PE⊥BC,ED⊥CD,若∠PDA=x°,∠PAD=y°,则∠C的度数为( )
如图,五边形ABCDE中,P为BC上一点,∠PAE=∠APE,∠DAE=∠ADE,且EA⊥BA,PE⊥BC,ED⊥CD,若∠PDA=x°,∠PAD=y°,则∠C的度数为( )| A、180°-2x° |
| B、180°-2y° |
| C、180°-x°-y° |
| D、90°+x°+y° |
方程2x2+3x=0解是( )
| A、x1=0,x2=-3 | ||
B、x1=0,x2=
| ||
C、x1=0,x2=-
| ||
D、x1=0,x2=-
|
下列二次根式是最简二次根式的个数是( )
①
;②
;③
;④
;⑤
;⑥
.
①
| 12 |
| a3b |
| x2+1 |
| 1.5 |
|
| ||
| 5 |
| A、4个 | B、3个 | C、2个 | D、1个 |
 如图,是一个10×10正方形网格纸,△ABC中A点的坐标为(2,4),B点的坐标为(1,1).
如图,是一个10×10正方形网格纸,△ABC中A点的坐标为(2,4),B点的坐标为(1,1).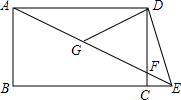 如图,点E是矩形ABCD边BC延长线上一点,AE交CD于F,G为AF中点.若∠DEA=2∠AEB,且DG=4,CE=1,则AB的长为( )
如图,点E是矩形ABCD边BC延长线上一点,AE交CD于F,G为AF中点.若∠DEA=2∠AEB,且DG=4,CE=1,则AB的长为( ) 在数轴上表示下列数,并用“<”号把这些数连接起来.
在数轴上表示下列数,并用“<”号把这些数连接起来.