题目内容
如图，在?ABCD中，BE=2AE，若S△AEF=6cm2，则S△ACD=考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：先根据?ABCD中，AE：EB=1：2得出AE：CD=1：3，再根据相似三角形的判定定理得出△AEF∽△CDF，由相似三角形的性质即可得出结论．
解答：解：∵?ABCD中，BE=2AE，
∴AE：CD=1：3，
∵AB∥CD，
∴∠EAF=∠DCF，∠DFC=∠AFE，
∴△AEF∽△CDF，
∴
=
=
，
∵S△AEF=6cm2，
∴
=（
）2=
，S△ADF=3S△AEF=18cm2，
则S△CDF=54cm2．
∴S△ACD=3S△AEF+S△CDF=72cm2．
故答案为：72cm2．
解：∵?ABCD中，BE=2AE，∴AE：CD=1：3，
∵AB∥CD，
∴∠EAF=∠DCF，∠DFC=∠AFE，
∴△AEF∽△CDF，
∴
| FE |
| ED |
| AE |
| CD |
| 1 |
| 3 |
∵S△AEF=6cm2，
∴
| S△AEF |
| S△CDF |
| 1 |
| 3 |
| 6 |
| S△CDF |
则S△CDF=54cm2．
∴S△ACD=3S△AEF+S△CDF=72cm2．
故答案为：72cm2．
点评：本题考查的是相似三角形的判定与性质，熟知相似三角形面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
相关题目
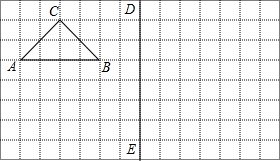如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：
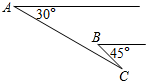有一位滑翔爱好者正在空中匀速向下滑翔，已知水平方向上的风速为5.8m/s，如图，在A点的他观察到C处塔尖的俯角为30°，5s后在B点的他观察到C处塔尖的俯角为45°，此时塔尖与他本人的距离BC是AC的