题目内容
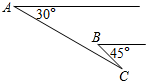 有一位滑翔爱好者正在空中匀速向下滑翔,已知水平方向上的风速为5.8m/s,如图,在A点的他观察到C处塔尖的俯角为30°,5s后在B点的他观察到C处塔尖的俯角为45°,此时塔尖与他本人的距离BC是AC的
有一位滑翔爱好者正在空中匀速向下滑翔,已知水平方向上的风速为5.8m/s,如图,在A点的他观察到C处塔尖的俯角为30°,5s后在B点的他观察到C处塔尖的俯角为45°,此时塔尖与他本人的距离BC是AC的| 1 |
| 4 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先过点B作BD⊥AD于点D,过点C作CE⊥AD于点E,则CF⊥BF,设BF=xm,则DE=xm,则可得方程:29+x=2
x,继而求得答案.
| 6 |
解答: 解:过点B作BD⊥AD于点D,过点C作CE⊥AD于点E,则CF⊥BF,
解:过点B作BD⊥AD于点D,过点C作CE⊥AD于点E,则CF⊥BF,
∴四边形BFED是矩形,
∴DE=BF,
设BF=xm,则DE=xm,
∵∠CBF=45°,
∴CF=BF=xm,
∴BC=
BF=
xm,
∵塔尖与他本人的距离BC是AC的
,
∴AC=4BC=4
m,
∴AE=AC•cos30°=2
xm,EC=AC•sin30°=2
x(cm),
∵水平方向上的风速为5.8m/s,
∴AD=5×5.8=29(m),
∴29+x=2
x,
解得:x=
,
∴DB=EF=EC-FC=2
x-x=
(m).
即此人的垂直下滑高度为:
m.
 解:过点B作BD⊥AD于点D,过点C作CE⊥AD于点E,则CF⊥BF,
解:过点B作BD⊥AD于点D,过点C作CE⊥AD于点E,则CF⊥BF,∴四边形BFED是矩形,
∴DE=BF,
设BF=xm,则DE=xm,
∵∠CBF=45°,
∴CF=BF=xm,
∴BC=
| 2 |
| 2 |
∵塔尖与他本人的距离BC是AC的
| 1 |
| 4 |
∴AC=4BC=4
| 2 |
∴AE=AC•cos30°=2
| 6 |
| 2 |
∵水平方向上的风速为5.8m/s,
∴AD=5×5.8=29(m),
∴29+x=2
| 6 |
解得:x=
29(2
| ||
| 23 |
∴DB=EF=EC-FC=2
| 2 |
29(8
| ||||||
| 23 |
即此人的垂直下滑高度为:
29(8
| ||||||
| 23 |
点评:本题考查俯角的定义,要求学生能借助俯角构造直角三角形并解直角三角形.注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各组运算中,结果为-4的是( )
| A、-(-4) |
| B、(-8)÷(-2) |
| C、|-4| |
| D、-22 |
 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A、BD=DC,AB=AC |
| B、∠ADB=∠ADC,BD=DC |
| C、∠B=∠C,∠BAD=∠CAD |
| D、∠B=∠C,BD=DC |
若|x|+x=0,则x一定是( )
| A、负数 | B、0 | C、非正数 | D、非负数 |
观察下列有规律的数:
,
,
,
,
,
…根据规律可知
(1)第7个数 ,第n个数是 (n是正整数);
(2)
是第 个数;
(3)计算
+
+
+
+…+
.
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| 30 |
| 1 |
| 42 |
(1)第7个数
(2)
| 1 |
| 132 |
(3)计算
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| 132 |
下列说法正确的是( )
| A、-8不是单项式 | ||||
B、单项式-
| ||||
| C、-3a2by3的次数是5 | ||||
D、-
|
 如图,在?ABCD中,BE=2AE,若S△AEF=6cm2,则S△ACD=
如图,在?ABCD中,BE=2AE,若S△AEF=6cm2,则S△ACD=