题目内容
14.(1)计算:$\sqrt{18}$-|-4|-2cos45°-(3-π)0.(2)先化简($\frac{1}{a-1}$-$\frac{1}{a+1}$)$÷\frac{a}{2{a}^{2}-2}$,然后从1、$\sqrt{2}$、-1中选取一个你认为合适的数作为a的值代入求值.
分析 (1)直接利用二次根式的性质和特殊角的三角函数值以及零指数幂的性质分别化简进而得出答案;
(2)直接将括号里面通分,进而利用分式混合运算法则求出答案.
解答 解:(1)$\sqrt{18}$-|-4|-2cos45°-(3-π)0
=3$\sqrt{2}$-4-2×$\frac{\sqrt{2}}{2}$-1
=2$\sqrt{2}$-5;
(2)($\frac{1}{a-1}$-$\frac{1}{a+1}$)$÷\frac{a}{2{a}^{2}-2}$
=[$\frac{a+1}{(a-1)(a+1)}$-$\frac{a-1}{(a+1)(a-1)}$]×$\frac{2(a+1)(a-1)}{a}$
=$\frac{2}{(a-1)(a+1)}$×$\frac{2(a+1)(a-1)}{a}$
=$\frac{4}{a}$,
由题意可得:a≠1,且a≠-1,
原式=$\frac{4}{a}$=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$.
点评 此题主要考查了实数运算以及分式的混合运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
4. 如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=( )
如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=( )
 如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=( )
如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=( )| A. | 35° | B. | 45° | C. | 70° | D. | 80° |
9. 如图,点A、B、C是⊙O上的三点,若∠BAC=50°,则∠OBC的度数是( )
如图,点A、B、C是⊙O上的三点,若∠BAC=50°,则∠OBC的度数是( )
 如图,点A、B、C是⊙O上的三点,若∠BAC=50°,则∠OBC的度数是( )
如图,点A、B、C是⊙O上的三点,若∠BAC=50°,则∠OBC的度数是( )| A. | 25° | B. | 40° | C. | 50° | D. | 80° |
4.若反比例函数y=-$\frac{4}{x}$的图象经过第二象限的点(a,-a),则a的值为( )
| A. | 2或-2 | B. | -2 | C. | 2 | D. | 4 |
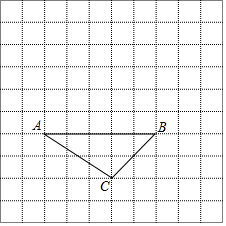 如图,已知△ABC.
如图,已知△ABC. 小新将一个有污渍的正方体纸盒沿如图所示的粗实线剪开,并展成平面图,其展开图为( )
小新将一个有污渍的正方体纸盒沿如图所示的粗实线剪开,并展成平面图,其展开图为( )


