题目内容
把一张矩形纸片,按如下图所示操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
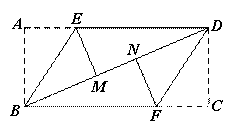
解:(1)证明:∵四边形ABCD是矩形,∴∠A=∠C=90°,AB=CD,AB∥CD,∴∠ABD=∠CDB,∴∠EBD=∠FDB,∴EB∥DF,∵ED∥BF,∴四边形BFDE是平行四边形.(2)如下图,若四边形BFDE为菱形,则∠EBD=∠CBD,又∵由翻折得∠ABE=∠EBD,又四边形ABCD是矩形,∴∠ABC=90°,∴∠ABE=30°,又∵AB=2,∴BE= ,∴菱形BFDE的面积为BF×AB=BE×AB=
,∴菱形BFDE的面积为BF×AB=BE×AB= ×2=
×2= .
.

练习册系列答案
相关题目
 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.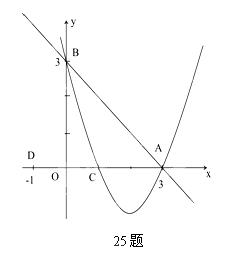
 的不等式组
的不等式组 的整数解共有3个,则
的整数解共有3个,则 的取值范围是 .
的取值范围是 .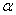 ,则sin
,则sin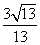 B.
B.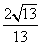 C.
C.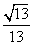 D.
D.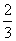
 (x>0)的图象与矩形OABC的边AB,BC分别交于点E,F,且AE=BE,则△OEF的面积为_______________.
(x>0)的图象与矩形OABC的边AB,BC分别交于点E,F,且AE=BE,则△OEF的面积为_______________.
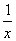 (x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;  ≤t≤1?
≤t≤1? 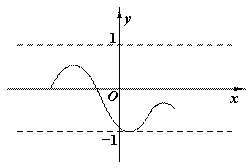
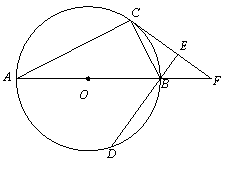
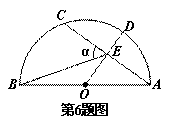
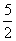 cm,弦BD的长为3 cm,求CF的长.
cm,弦BD的长为3 cm,求CF的长.