题目内容
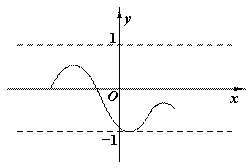
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M<y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
(1)分别判断函数y=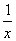 (x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;
(3)将函数y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足 ≤t≤1?
≤t≤1?
 (2)∵函数y=﹣x+1的图象是y随x的增大而减小,
(2)∵函数y=﹣x+1的图象是y随x的增大而减小,
∴当x=a时,y=﹣a+1,
又边界值为2,∴﹣a+1=2,解得a=﹣1,
当x=b时,y=﹣b+1,则﹣2≤﹣b+1≤2,
又b>a,a=﹣1,
∴解得﹣1<b≤3.
(3)若m>1,函数向下平移m个单位后,x=0时,函数值小于﹣1,
此时函数的边界值t≥1,这与题意不符,∴m≤1.
当x=﹣1时,y=1,即过点(﹣1,1),
当x=0时,y最小=0,即过点(0,0),
都向下平移m个单位,则对应点的坐标为(﹣1,1-m),(0,﹣m),
由边界值定义可得 ≤1-m≤1或﹣1≤﹣m≤﹣
≤1-m≤1或﹣1≤﹣m≤﹣ ,
,
∴解得0≤m≤ 或
或 ≤m≤1.
≤m≤1.

练习册系列答案
相关题目

 的结果______________________.
的结果______________________.
 ,那么x2– y2= .
,那么x2– y2= .



 .
.