题目内容
如图，反比例函数y＝
（x＞0）的图象与矩形OABC的边AB，BC分别交于点E，F，且AE＝BE，则△OEF的面积为_______________.
解析：∵点E在反比例函数图象上，∴设E（x，），∵AB∥y轴，AE＝BE，∴B点坐标为（x，
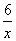），又∵BC∥x轴，F为BC与双曲线的交点，∴F点坐标为（
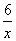，），∴BF＝CF，由反比例函数的意义可得S△AOE＝
，连接OB，可得OF，OE分别为△BOC，△AOB的中位线，∴S△COF＝S△AOE＝
S矩形OABC，∴S矩形OABC＝4S△COF＝4×
＝6，又∵S△BEF＝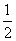
S△AOE，∴S△BEF＝
S矩形OABC＝×6＝
，∴S△OEF＝S矩形OABC－S△COF－S△AOE＝S△BEF＝6——－＝. 21*cnjy*com
练习册系列答案
应用题作业本系列答案
相关题目
___________；
，
四个数中，是无理数的是…………………………【 】
C. 
B．
C．
D．
，其中m = 4.
；④在对称轴左侧，y随x的增大而增大．