题目内容
甲、乙两人由A地到B地,甲先走2小时乙再出发,结果乙比甲晚到15分钟,已知甲的速度为每小时4千米,乙的速度为每小时6千米,求A,B两地的距离.
考点:一元一次方程的应用
专题:
分析:设A,B两地的距离为xkm,则甲需要的时间为
小时,乙需要的时间为
小时,由甲先走2小时乙再出发,结果乙比甲晚到15分钟,可得甲比乙多用2-
=
小时,根据甲乙的时间关系建立方程求出其解即可.
| x |
| 4 |
| x |
| 6 |
| 1 |
| 4 |
| 7 |
| 4 |
解答:解:设A,B两地的距离为xkm,则甲需要的时间为
小时,乙需要的时间为
小时,
根据题意得:
-
=2-
,
解得:x=21.
答:A,B两地的距离为21千米.
| x |
| 4 |
| x |
| 6 |
根据题意得:
| x |
| 4 |
| x |
| 6 |
| 15 |
| 60 |
解得:x=21.
答:A,B两地的距离为21千米.
点评:本题考查了列一元一次方程解实际问题的运用,行程问题的数量关系的运用,根据时间之间的数量关系建立方程是关键.

练习册系列答案
相关题目
若等式4a-3b=0成立,则下列等式成立的是( )
| A、4a+3=3b+4 | ||||
| B、3a=4b | ||||
| C、4a=3b | ||||
D、
|
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(0,-3),且对称轴为x=2,则这条抛物线的顶点坐标为( )
| A、(2,3) |
| B、(2,1) |
| C、(-2,1) |
| D、(2,-1) |
 如图四边形ABCD,以AB为边作△ABM,使S△ABM=S四边形ABCD.
如图四边形ABCD,以AB为边作△ABM,使S△ABM=S四边形ABCD.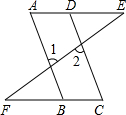 如图,请你从①∠1=∠2;②AD∥BC;③∠A=∠C;④∠ABF=∠E中,选取其中两个作为条件,一个作为结论,构成一个真命题,并加以证明.选取的条件是
如图,请你从①∠1=∠2;②AD∥BC;③∠A=∠C;④∠ABF=∠E中,选取其中两个作为条件,一个作为结论,构成一个真命题,并加以证明.选取的条件是