题目内容
14．已知等边△ABC的边长为2．（1）以其中一边所在的直线为轴旋转一周，分析所形成的几何体的结钩特征；
（2）以其中一边上的中线所在的直线为轴旋转一周，分析所形成的几何体的结构特征．
分析 （1）根据题目中的描述可以得到所形成的几何体的结钩特征；
（2）根据题目中的描述可以得到所形成的几何体的结钩特征．
解答 解：（1）以等边△ABC其中一边所在的直线为轴旋转一周，所形成的几何体是两个母线长为2，底面半径为$\sqrt{3}$的圆锥对在一起的组合体；
（2）以等边△ABC其中一边上的中线所在的直线为轴旋转一周，所形成的几何体是母线长为2，底面半径为1的圆锥．
点评 本题考查点、线、面、体，等边三角形的性质，解题的关键是明确题意，可以想象出旋转后形成的几何体的结构特征．
练习册系列答案
相关题目
4．25的平方根是（ ）
| A． | 5 | B． | -5 | C． | ±5 | D． | 10 |
甲、乙两同学从A地出发，骑自行车在同一路上行驶到B地，他们离出发地的距离s（千米）与行驶的时间t（小时） 之间的函数关系如图所示，根据图中提供的信息，有下列说法：
2．
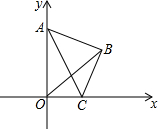如图，在平面直角坐标系中，已知AB=BC，∠ABC=90°，若点A落在y轴上，点C落在x轴上，△ABC的形状始终不变，随着点C由原点O向x轴正半轴方向运动，点A沿y轴负半轴方向运动到终点O，在此次运动过程中，线段OB的长度变化情况是（ ）
如图，在平面直角坐标系中，已知AB=BC，∠ABC=90°，若点A落在y轴上，点C落在x轴上，△ABC的形状始终不变，随着点C由原点O向x轴正半轴方向运动，点A沿y轴负半轴方向运动到终点O，在此次运动过程中，线段OB的长度变化情况是（ ）| A． | 一直增大 | B． | 一直减小 | C． | 先减小后增大 | D． | 先增大后减小 |
9．下列关于正比例函数y=3x的说法中，正确的是（ ）
| A． | 当x=3时，y=1 | B． | 它的图象是一条过原点的直线 | ||
| C． | y随x的增大而减小 | D． | 它的图象经过第二、四象限 |
19．某同学使用计算器求30个数据的平均数时，错将其中的一个数据105输入为15，那么由此求出的平均数与实际平均数的差是（ ）
| A． | -3.5 | B． | 3 | C． | 0.5 | D． | -3 |
6．
如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，点P是线段AB上的一动点，将△ABC绕点C按顺时针方向旋转，得到△A1B1C1，点E是线段A1C的中点，则PE长度的最小值为（ ）
如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，点P是线段AB上的一动点，将△ABC绕点C按顺时针方向旋转，得到△A1B1C1，点E是线段A1C的中点，则PE长度的最小值为（ ）| A． | $\sqrt{2}$-1 | B． | $\sqrt{3}$-1 | C． | $\sqrt{2}$+1 | D． | $\sqrt{3}$+1 |
4．下列图形中，是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |