题目内容
10.在平面直角坐标系中,顶点为(3,4)的抛物线交y轴与A点,交x轴与B、C两点(点B在点C的左侧),已知A点坐标为(0,-5),求此抛物线的解析式.分析 根据抛物线的顶点坐标为(3,4)设出其解析式,再把A点坐标代入即可得出结论.
解答 解:∵抛物线的顶点坐标为(3,4),
∴设抛物线的解析式为y=a(x-3)2+4.
∵A点坐标为(0,-5),
∴a(0-3)2+4=-5,解得a=-1,
∴此抛物线的解析式为:y=-(x-3)2+4.
点评 本题考查的是待定系数法求二次函数的解析式,熟知抛物线的顶点式是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
15.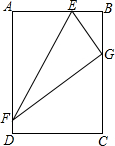 如图,矩形ABCD的边AB有一点E,AE:EB=3:2,DA边上有点F,且EF=18,将矩形沿EF对折后,点A落在边BC上的点G,则AB为( )
如图,矩形ABCD的边AB有一点E,AE:EB=3:2,DA边上有点F,且EF=18,将矩形沿EF对折后,点A落在边BC上的点G,则AB为( )
 如图,矩形ABCD的边AB有一点E,AE:EB=3:2,DA边上有点F,且EF=18,将矩形沿EF对折后,点A落在边BC上的点G,则AB为( )
如图,矩形ABCD的边AB有一点E,AE:EB=3:2,DA边上有点F,且EF=18,将矩形沿EF对折后,点A落在边BC上的点G,则AB为( )| A. | 3$\sqrt{6}$ | B. | 5$\sqrt{6}$ | C. | 5$\sqrt{3}$ | D. | 6$\sqrt{2}$ |
20. 如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )
如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )
 如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )
如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )| A. | -$\frac{2}{3}$ | B. | -$\frac{2\sqrt{3}}{3}$ | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
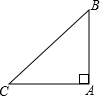 如图,在Rt△ABC中,∠BAC=90°,AB=AC.
如图,在Rt△ABC中,∠BAC=90°,AB=AC.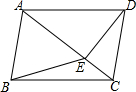 如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.