题目内容
 已知ABCD为正方形,E、F分别是AD、CD上的一点,∠EBF=45°,△EFD周长为2,求正方形边长.
已知ABCD为正方形,E、F分别是AD、CD上的一点,∠EBF=45°,△EFD周长为2,求正方形边长.考点:旋转的性质,全等三角形的判定与性质,正方形的性质
专题:
分析:如图,作辅助线;首先证明△ABF≌△CBG,进而证明∠EBG=∠ABF+∠EBC=45°;再次证明△EBG≌△EBF得到EF=EG=AF+EC,结合△EFD周长为2,即可解决问题.
解答: 解:如图,延长DC到G,使CG=AF;
解:如图,延长DC到G,使CG=AF;
∵四边形ABCD为正方形,
∴AB=BC,∠A=∠C=90°;
在△ABF与△CBG中,
,
∴△ABF≌△CBG(SAS),
∴∠ABF=∠CBG,BF=BG;
∴∠GBE=∠ABF+∠EBC;
∵∠EBF=45°,
∴∠ABF+∠EBC=90°-45°=45°,
∴∠EBG=∠EBF;
在△EBG与△EBF中,
,
∴△EBG≌△EBF(SAS),
∴EF=EG=AF+EC,
∴△EFD周长=2AD=2,
∴正方形的边长为1.
 解:如图,延长DC到G,使CG=AF;
解:如图,延长DC到G,使CG=AF;∵四边形ABCD为正方形,
∴AB=BC,∠A=∠C=90°;
在△ABF与△CBG中,
|
∴△ABF≌△CBG(SAS),
∴∠ABF=∠CBG,BF=BG;
∴∠GBE=∠ABF+∠EBC;
∵∠EBF=45°,
∴∠ABF+∠EBC=90°-45°=45°,
∴∠EBG=∠EBF;
在△EBG与△EBF中,
|
∴△EBG≌△EBF(SAS),
∴EF=EG=AF+EC,
∴△EFD周长=2AD=2,
∴正方形的边长为1.
点评:该题主要考查了正方形的性质、全等三角形的判定及其性质等知识的应用问题;解题的关键是作辅助线,构造全等三角形.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从点C开始沿CB向点B以1cm/s的速度移动,点Q从A开始沿AC向点C以2cm/s的速度移动,如果点P,Q同时从点C,A出发,试问:
如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从点C开始沿CB向点B以1cm/s的速度移动,点Q从A开始沿AC向点C以2cm/s的速度移动,如果点P,Q同时从点C,A出发,试问: 阅读下列内容:
阅读下列内容: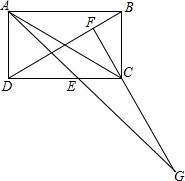 如图,矩形ABCD中,过C作CF⊥BD于F,延长FC至G,CG=BD,连AG交CD于E,∠AED的度数是多少?
如图,矩形ABCD中,过C作CF⊥BD于F,延长FC至G,CG=BD,连AG交CD于E,∠AED的度数是多少?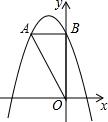 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA. (1)与∠E成内错角的是
(1)与∠E成内错角的是 如图,AB⊥CD,垂足为O,EF经过点O,∠2=2∠1,求∠2,∠3,∠BOE的度数.
如图,AB⊥CD,垂足为O,EF经过点O,∠2=2∠1,求∠2,∠3,∠BOE的度数. 如图,AF平分∠DAC,BF平分∠DBC,若AD∥BC,∠C+∠D=2∠F是否成立?请予以说明.
如图,AF平分∠DAC,BF平分∠DBC,若AD∥BC,∠C+∠D=2∠F是否成立?请予以说明. 如图,OA⊥OB,OC⊥OD,∠AOE=∠COE,求证:OE平分∠BOD.
如图,OA⊥OB,OC⊥OD,∠AOE=∠COE,求证:OE平分∠BOD.