题目内容
4.已知方程2x2-3x-4=0的两个根是x1,x2,求下列各式的值.(1)x12+x1x2+x22; (2)$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$.
分析 (1)根据根与系数的关系得出x1+x2=$\frac{3}{2}$,x1•x2=-2,变形后代入求出即可;
(2)先通分,再变形后代入求出即可.
解答 解:(1)∵方程2x2-3x-4=0的两个根是x1,x2,
∴x1+x2=$\frac{3}{2}$,x1•x2=-2,
∴x12+x1x2+x22;=(x1+x2)2-x1x2
=($\frac{3}{2}$)2-(-2)
=4$\frac{1}{2}$;
(2)∵x1+x2=$\frac{3}{2}$,x1•x2=-2,
∴$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$
=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$
=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$
=$\frac{(\frac{3}{2})^{2}-2×(-2)}{-2}$
=-$\frac{25}{8}$.
点评 本题考查了根与系数关系,完全平方公式的应用,能熟记根与系数关系的内容是解此题的关键,若x1、x2是一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0)的两个根,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
15.三角形的两边长分别为3和6,第三边的长是方程x2-6x+8=0的一个根,则这个三角形的周长是( )
| A. | 9 | B. | 11 | C. | 13 | D. | 11或13 |
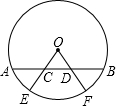 已知:如图,AB是⊙O的弦,且AC=BD,半径OE,OF分别过C,D两点,求证:$\widehat{AE}$=$\widehat{BF}$.
已知:如图,AB是⊙O的弦,且AC=BD,半径OE,OF分别过C,D两点,求证:$\widehat{AE}$=$\widehat{BF}$.