题目内容
 已知,如图,OA,OB为⊙0的半径,C,D分别为OA,OB的中点.求证:
已知,如图,OA,OB为⊙0的半径,C,D分别为OA,OB的中点.求证:(l)∠A=∠B;
(2)AE=BE.
考点:全等三角形的判定与性质,圆的认识
专题:证明题
分析:(1)首先根据全等三角形的判定方法证明△AOD≌△BOC,由全等三角形的性质即可得到∠A=∠B;
(2)由(1)可知∠A=∠B再加条件对顶角相等即可证明△ACE≌△BDE,利用全等三角形的性质即可证明AE=BE.
(2)由(1)可知∠A=∠B再加条件对顶角相等即可证明△ACE≌△BDE,利用全等三角形的性质即可证明AE=BE.
解答:(1)证明:∵C、D是OA、OB的中点,
∴OC=OD=AC=BD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS)
∴∠A=∠B;
(2)在△ACE和△BDE中,
,
∴△ACE≌△BDE(AAS),
∴AE=BE.
∴OC=OD=AC=BD,
在△AOD和△BOC中,
|
∴△AOD≌△BOC(SAS)
∴∠A=∠B;
(2)在△ACE和△BDE中,
|
∴△ACE≌△BDE(AAS),
∴AE=BE.
点评:本题考查了全等三角形的判定和性质以及圆的基本性质,其中全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
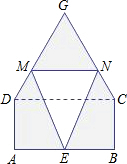 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部△CDG是等腰三角形,固定点E为AB的中点.GE最大高度为3米,△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.设MN到AB之间距离为x米(0≤x≤3)
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部△CDG是等腰三角形,固定点E为AB的中点.GE最大高度为3米,△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.设MN到AB之间距离为x米(0≤x≤3)