题目内容
二次函数y=x2-2x-3的图象与x轴交于A、B两点，与y轴交于点C，求S△ABC的面积．
考点：抛物线与x轴的交点
专题：
分析：首先根据题意得出求出图象与x轴以及y轴交点坐标，即可求出AB，CO长，即可求出S△ABC的值．
解答：
解：当y=0时，x2-2x-3=0，
∴（x+1）（x-3）=0，
解得：x1=-1，x2=3，
∴AB=3-（-1）=4，
当x=0时，y=-3，
∴CO=3，
∴S△ABC=
×3×4=6．
解：当y=0时，x2-2x-3=0，∴（x+1）（x-3）=0，
解得：x1=-1，x2=3，
∴AB=3-（-1）=4，
当x=0时，y=-3，
∴CO=3，
∴S△ABC=
| 1 |
| 2 |
点评：此题主要考查了抛物线与x轴的交点，得出图象与坐标轴交点是解题关键．
练习册系列答案
特高级教师点拨系列答案
相关题目
如图，C是线段BD的中点，AD=3，AC=7，求线段AB的长．
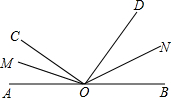如图，∠AOB是平角，OM、ON分别是∠AOC、∠BOD的平分线． 且∠AOC=40°，∠BOD=50°．求：
如图：△ABC和△CDE是等边三角形．求证：BE=AD．
已知，如图，OA，OB为⊙0的半径，C，D分别为OA，OB的中点．求证：