题目内容

3．不论a，b为何实数，a2+b2-2a-4b+8的值（　　）
A．总是正数B．总是负数
C．可以是零D．可以是正数也可以是负数

分析 原式配方后，利用完全平方公式变形，根据完全平方式恒大于等于0，判断即可得到结果．

解答 解：a2+b2-2a-4b+8=（a2-2a+1）+（b2-4b+4）+3=（a-1）2+（b+2）2+3，
∵（a-1）2≥0，（b+2）2≥0，
∴（a-1）2+（b+2）2+3≥3，
则不论a、b为任何实数，式子a2+b2-2a-4b+8的值总不小于3．
故选A．

点评 此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．

练习册系列答案
相关题目
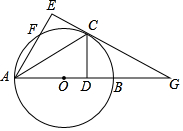14．如图，AB是⊙O的直径，C为⊙O上一点，CD垂直AB于D，把△ACD沿直线AC折叠得到△ACE，AE交⊙O于F点，EC、AB的延长线交于G
（1）求证：CE与⊙O相切；
（2）如果AB=4，∠BAC=30°，求CG、BG的长．
14．对于实数x，y，定义一种运算“*”如下，x*y=ax-by2，已知2*3=10，4*（-3）=6，那么（-2）*2=$\frac{92}{9}$．
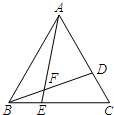11．已知△ABC是等边三角形，点D、E分别在AC、BC上，且CD=BE，则∠BFE=60°．
18．平面内两两相交的8条直线，其交点个数最少为m个，最多为n个，则m+n等于（　　）
A．16B．18C．29D．28
8．汽车刹车后行驶的距离s（单位：m）关于行驶的时间t（单位：秒）的函数解析式是s=6t-4t2，当汽车刹车后到停下来前进了$\frac{9}{4}$米．
15．下列说法中，正确的个数有（　　）
（1）-a一定是负数；
（2）|-a|一定是正数；
（3）倒数等它本身的数是±1；
（4）绝对值等于它本身的数是1；
（5）两个有理数的和一定大于其中每一个加数；
（6）a的指数是0；
（7）-0.3＞-0.2．
A．1个B．2个C．3个D．4个
12．若abc＞0，则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|abc|}{abc}$的值为（　　）
A．±4B．4或0C．±2D．±4或0
13．（1）$\sqrt{{5}^{2}+1{2}^{2}}$=13'
（2）$\sqrt{81}$的平方根是±3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网