题目内容
12.若abc>0,则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|abc|}{abc}$的值为( )| A. | ±4 | B. | 4或0 | C. | ±2 | D. | ±4或0 |
分析 根据题意可以得到关于a、b、c的符号,从而可以得到题目中所求式子的值,本题得以解决.
解答 解:∵abc>0,
∴a、b、c均为正数或a、b、c中一正两负,
∴当、b、c均为正数时,
$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|abc|}{abc}$=$\frac{a}{a}+\frac{b}{b}+\frac{c}{c}+\frac{abc}{abc}$+1+1+1+1=4,
当a、b、c中一正两负,假设a>0,b<0,c<0,
$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|abc|}{abc}$=$\frac{a}{a}+\frac{-b}{b}+\frac{-c}{c}+\frac{abc}{abc}$=1-1-1+1=0,
由上可得,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|abc|}{abc}$的值是4或0,
故选B.
点评 本题考查绝对值,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
2.定义运算“*”,规定x*y=ax+by2,其中a、b为常数,且1*2=11,2*1=1,则2*3=( )
| A. | -3 | B. | 5 | C. | 25 | D. | 29 |
3.不论a,b为何实数,a2+b2-2a-4b+8的值( )
| A. | 总是正数 | B. | 总是负数 | ||
| C. | 可以是零 | D. | 可以是正数也可以是负数 |
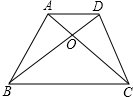 如图,已知梯形ABCD的面积为S,AD∥BC,BC=b,AD=a(a<b),对角线AC与BD交于点O.若△COD的面积为$\frac{2}{9}$S,则$\frac{a}{b}$=$\frac{1}{2}$.
如图,已知梯形ABCD的面积为S,AD∥BC,BC=b,AD=a(a<b),对角线AC与BD交于点O.若△COD的面积为$\frac{2}{9}$S,则$\frac{a}{b}$=$\frac{1}{2}$.