题目内容
如图,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度在直线AM上运动;已知AC=6cm,设动点D,E的运动时间为t.
(1)试求∠ACB的度数;
(2)若S△ABD:S△BEC=2:3,试求动点D,E的运动时间t的值;
(3)试问当动点D,E在运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
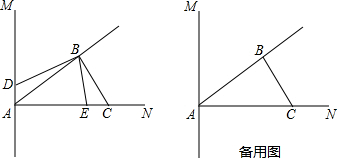
(1)试求∠ACB的度数;
(2)若S△ABD:S△BEC=2:3,试求动点D,E的运动时间t的值;
(3)试问当动点D,E在运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.

考点:全等三角形的判定与性质,坐标与图形性质
专题:动点型
分析:(1)易求∠BAC=45°,根据BC⊥BA可得∠ABC=90°,即可解题;
(2)作BF⊥AM,BG⊥AC,则BF=BG,根据S△ABD:S△BEC的值可得AD:CE的值,分别用t表示AD,CE即可求得t的值,即可解题;
(3)易得AD=CE时,△ADB≌△BEC,分别用t表示AD,CE即可求得t的值,即可解题.
(2)作BF⊥AM,BG⊥AC,则BF=BG,根据S△ABD:S△BEC的值可得AD:CE的值,分别用t表示AD,CE即可求得t的值,即可解题;
(3)易得AD=CE时,△ADB≌△BEC,分别用t表示AD,CE即可求得t的值,即可解题.
解答:解:(1)∵AM⊥AN,AB平分∠MAN,
∴∠BAC=45°,
∵BC⊥BA,∴∠ABC=90°,
∴∠ACB=45°;
(2)作BF⊥AM,BG⊥AC,则BF=BG,
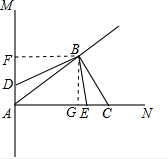
∵S△ABD:S△BEC=2:3,
∴AD:CE=2:3,
∵AD=t,CE=6-2t,
∴3t=2(6-2t),
解得:t=
s;
(3)∵AB=BC,∠BAM=∠BCA=45°,
∴AD=CE即可证明△ADB≌△BEC,(SAS)
∴6-2t=t,或2t-6=t,
解得:t=2,或t=6,
当t=6时,∠BCE=135°,∠BAD=45°,故t=6不符合题意,舍去,
答:t=2时,△ADB≌△BEC.
∴∠BAC=45°,
∵BC⊥BA,∴∠ABC=90°,
∴∠ACB=45°;
(2)作BF⊥AM,BG⊥AC,则BF=BG,

∵S△ABD:S△BEC=2:3,
∴AD:CE=2:3,
∵AD=t,CE=6-2t,
∴3t=2(6-2t),
解得:t=
| 12 |
| 7 |
(3)∵AB=BC,∠BAM=∠BCA=45°,
∴AD=CE即可证明△ADB≌△BEC,(SAS)
∴6-2t=t,或2t-6=t,
解得:t=2,或t=6,
当t=6时,∠BCE=135°,∠BAD=45°,故t=6不符合题意,舍去,
答:t=2时,△ADB≌△BEC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中找出求证△ADB≌△BEC的条件是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
如果x>y,那么下列选项正确的是( )
| A、-3x>-3y | ||||
B、
| ||||
| C、x2>y2 | ||||
| D、x-5>y-5 |
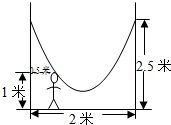 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.| A、0.5 | B、0.6 |
| C、1 | D、1.5 |
若A=2x2-8x,B=x2+2x+1,则使A-2B=-10的x的值是( )
A、
| ||
| B、3 | ||
C、
| ||
D、
|
 如图,已知AD=BC,AB=DC,DE=BF,求证:BE=DF.
如图,已知AD=BC,AB=DC,DE=BF,求证:BE=DF. 如图,设△ABC是等腰直角三角形,BC=AC,D是斜边AB的中点,E、F分别是AC、BC边上的点,且DE⊥DF,若BF=10,CF=5,则线段EF=
如图,设△ABC是等腰直角三角形,BC=AC,D是斜边AB的中点,E、F分别是AC、BC边上的点,且DE⊥DF,若BF=10,CF=5,则线段EF= 如图,已知三点A、B、Q,请画直线AB,并描述点Q和直线AB的位置关系:
如图,已知三点A、B、Q,请画直线AB,并描述点Q和直线AB的位置关系: