题目内容
如图，已知AD=BC，AB=DC，DE=BF，求证：BE=DF．考点：全等三角形的判定与性质
专题：证明题
分析：易证四边形ABCD为平行四边形，可得AD∥BC，即可求得∠EDB=∠FBD，即可证明△BDF≌△DBE，可得BE=DF，即可解题．
解答：证明：∵AD=BC，AB=DC，
∴四边形ABCD为平行四边形，
∴AD∥BC，
∴∠EDB=∠FBD，
∵在△BDF和△DBE中，
，
∴△BDF≌△DBE，（SAS）
∴BE=DF．
∴四边形ABCD为平行四边形，
∴AD∥BC，
∴∠EDB=∠FBD，
∵在△BDF和△DBE中，
|
∴△BDF≌△DBE，（SAS）
∴BE=DF．
点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△BDF≌△DBE是解题的关键．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）．
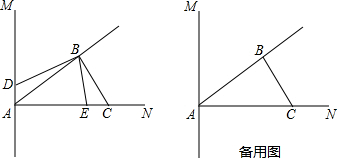
如图，直角三角形ABC的斜边AB在直线l上，把△ABC按顺时针方向在l上转动两次，使它转到△A′B′C′的位置，设BC=1，AC=