题目内容
19. 如图,已知AB是⊙O的直径,CD⊥AB,垂足为D,AE⊥AB,且AE=AC,BE交⊙O于点F.求证:EF•EB=AD•AB.
如图,已知AB是⊙O的直径,CD⊥AB,垂足为D,AE⊥AB,且AE=AC,BE交⊙O于点F.求证:EF•EB=AD•AB.
分析 连接BC,AF,由圆周角定理得到∠ACB=∠AFB=90°,由垂直的定义得到∠ADC=∠EAB=90°,推出△ACD∽△ABC,根据相似三角形的性质得到$\frac{AC}{AB}=\frac{AD}{AC}$,于是得到AC2=AD•AB,同理得到AE2EF•EB,等量代换即可得到结论.
解答 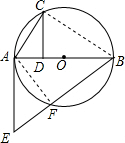 证明:连接BC,AF,
证明:连接BC,AF,
∵AB是⊙O的直径,
∴∠ACB=∠AFB=90°,
∵CD⊥AB,AE⊥AB,
∴∠ADC=∠EAB=90°,
∴∠ADC=∠ACB,
∵∠CAB=∠BAC,
∴△ACD∽△ABC,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∴AC2=AD•AB,
∵∠EAB=∠AFE,∠E=∠E,
∴△AEF∽△ABF,
∴$\frac{AE}{BE}=\frac{EF}{AE}$,
∴AE2EF•EB,
∵AC=AE,
∴EF•EB=AD•AB.
点评 本题考查了相似三角形的判定和性质,圆周角定理,垂直的定义,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列图形是轴对称图形的是( )
| A. | 人的两点手 | B. | 两个1圆硬币 | C. | 线段 | D. | 平行四边形 |
 一个实物几何体的俯视图如下图所示,其中每个正方形的数字表示该位置上正方体的个数.请画出相应的主视图和左视图.
一个实物几何体的俯视图如下图所示,其中每个正方形的数字表示该位置上正方体的个数.请画出相应的主视图和左视图.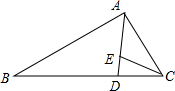 如图,在△ABC中,若∠DAC=∠B.
如图,在△ABC中,若∠DAC=∠B.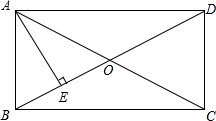 如图,在矩形ABCD中,AE⊥BD,垂足为E,BE与ED的长度之比为1:3,则tan∠ADB=$\frac{\sqrt{3}}{3}$.
如图,在矩形ABCD中,AE⊥BD,垂足为E,BE与ED的长度之比为1:3,则tan∠ADB=$\frac{\sqrt{3}}{3}$.