题目内容
求多项式(2x3-5x2+x+1)3•(
x-1)2的展开式中各项系数之和.
| 2 |
| 3 |
考点:多项式乘多项式
专题:计算题
分析:利用赋值法:令多项式中的x=1得各项系数和,即可得出结果.
解答:解:(1)设f(x)=(3x3-5x2+x+1)3•(
x-1)2
=a0+a1x+a2x2+…+anxn(n∈N),
其各项系数和为a0+a1+a2+…+an.
又∵f(1)=a0+a1+a2++an=(2-5+1+1)3•(
-1)2=-
,
∴各项系数和为-
.
| 2 |
| 3 |
=a0+a1x+a2x2+…+anxn(n∈N),
其各项系数和为a0+a1+a2+…+an.
又∵f(1)=a0+a1+a2++an=(2-5+1+1)3•(
| 2 |
| 3 |
| 1 |
| 9 |
∴各项系数和为-
| 1 |
| 9 |
点评:此题考查了多项式乘多项式;用赋值法求多项式展开式的系数和是解题的关键.

练习册系列答案
相关题目
-125开立方,结果是( )
| A、±5 | |||
| B、5 | |||
| C、-5 | |||
D、±
|
如图,是一个简单的数值运算程序,当输入x的值为-2,则输出的数值为( )

| A、26 | B、24 | C、22 | D、18 |
 如图,直线y=x+2分别与x轴、y轴交于点A、B,将直线AB沿y轴向下平移至点C(0,-1),与x轴交于点D,过点B作BE⊥CD,垂足为E.
如图,直线y=x+2分别与x轴、y轴交于点A、B,将直线AB沿y轴向下平移至点C(0,-1),与x轴交于点D,过点B作BE⊥CD,垂足为E.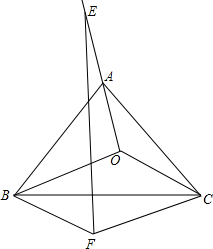 已知O是等边三角形ABC所在平面上任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC连接EF,请探索FE与BC之间的关系.
已知O是等边三角形ABC所在平面上任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC连接EF,请探索FE与BC之间的关系. 如图,已知点D是⊙O外的一点,DA为⊙O的切线,A为切点,AB为⊙O的直径,BD交⊙O于点C,若DA=4,DC=2,求图中阴影部分面积.
如图,已知点D是⊙O外的一点,DA为⊙O的切线,A为切点,AB为⊙O的直径,BD交⊙O于点C,若DA=4,DC=2,求图中阴影部分面积. 已知一个立体图形的三视图如图所示,现沿它的同一顶点的三条棱将其剪开展成平面图形,则所得到的平面展开图是下列图中的( )
已知一个立体图形的三视图如图所示,现沿它的同一顶点的三条棱将其剪开展成平面图形,则所得到的平面展开图是下列图中的( )



 如图,AB∥CD,∠B:∠O:∠D=4:3:3,则∠B=
如图,AB∥CD,∠B:∠O:∠D=4:3:3,则∠B=