题目内容
20.先化简,再求值:($\frac{{x}^{2}}{x-1}$$-\frac{{x}^{2}}{{x}^{2}-1}$)÷$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$,其中x是方程x2-2x-2=0的根.分析 首先把所求的式子中括号内的分式通分相加,然后把除法转化为乘法,计算乘法即可化简,然后根据x2-2x-2=0得到x2=2(x+1),代入求值即可.
解答 解:原式=[$\frac{{x}^{2}(x+1)}{{x}^{2}-1}$-$\frac{{x}^{2}}{{x}^{2}-1}$]•$\frac{(x-1)^{2}}{x(x-1)}$
=$\frac{{x}^{3}}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x(x-1)}$
=$\frac{{x}^{2}}{x+1}$.
∵x2-2x-2=0,
∴x2=2(x+1),
∴原式=$\frac{2(x+1)}{x+1}$=2.
点评 本题考查了分式的化简求值以及方程的解的定义,正确对已知的分式进行通分、约分是关键.

练习册系列答案
相关题目
10.下列写法正确的是( )
| A. | x5 | B. | 4m×n | C. | 1$\frac{3}{4}$m | D. | -$\frac{1}{2}$ab |
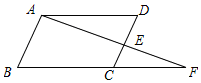 根据解答过程填空(写出推理理由或根据):
根据解答过程填空(写出推理理由或根据):