题目内容
 如图,矩形ABCD中,AB=2,BC=2
如图,矩形ABCD中,AB=2,BC=2| 3 |
| 1 |
| 2 |
考点:直线与圆的位置关系
专题:计算题
分析:在Rt△ABC利用勾股定理计算出AC=4,先计算⊙O与AB相切时OA的长,如图,作OH⊥AB于H,则根据切线的性质得OH=
,利用OH∥BC,根据平行线分线段成比例可计算出OA=
,然后根据直线与相交的判定方法易得当0≤m<4时,BA与⊙O相交.
| 1 |
| 2 |
| 3 |
解答:解:在Rt△ABC,∵AB=2,BC=2
,
∴AC=
=4,
当⊙O与AB相切,如图,作OH⊥AB于H, 则OH=
则OH=
,
∵OH∥BC,
∴
=
,即
=
,
∴OA=
,
∴当0≤OA<4,BA与⊙O相交,
即0≤m<4.
| 3 |
∴AC=
| AB2+BC2 |
当⊙O与AB相切,如图,作OH⊥AB于H,
 则OH=
则OH=| 1 |
| 2 |
∵OH∥BC,
∴
| AO |
| AC |
| OH |
| BC |
| OA |
| 4 |
| ||
2
|
∴OA=
| 3 |
∴当0≤OA<4,BA与⊙O相交,
即0≤m<4.
点评:本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
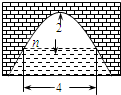 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加( )
如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加( )| A、1m | ||
| B、2m | ||
C、(2
| ||
D、(
|
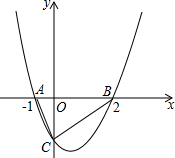 如图:抛物线与x轴交于点A(-1,0),B(2,0).与y轴的负半轴交于点C,且△ABC的面积为3
如图:抛物线与x轴交于点A(-1,0),B(2,0).与y轴的负半轴交于点C,且△ABC的面积为3 如图,D是△ABC的BC边上的一点,过点D的一条直线交AC于点F,交BA的延长线于点E,若BD=CD,CF=2AF,则EA:EB=
如图,D是△ABC的BC边上的一点,过点D的一条直线交AC于点F,交BA的延长线于点E,若BD=CD,CF=2AF,则EA:EB= 如图,已知在圆内接四边形ABCD中,∠CAD=∠CAB=60°,求证:△BDC是等边三角形.
如图,已知在圆内接四边形ABCD中,∠CAD=∠CAB=60°,求证:△BDC是等边三角形.