题目内容
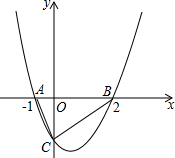 如图:抛物线与x轴交于点A(-1,0),B(2,0).与y轴的负半轴交于点C,且△ABC的面积为3
如图:抛物线与x轴交于点A(-1,0),B(2,0).与y轴的负半轴交于点C,且△ABC的面积为3(1)求点C的坐标;
(2)求此抛物线的解析式;
(3)在x轴下方的抛物线上是否存在点P,使得以A,B,P为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)利用三角形的面积公式求得OC的长度,则易求点C的坐标;
(2)把点A、B、C的坐标分别代入二次函数解析式,列出关于系数的方程组,通过解方程组来求系数的值.即利用待定系数法来求二次函数的解析式;
(3)两个三角形中的公共边是线段AB,且线段AB是抛物线以下△PAB中最大的一条边,那就说明AB边只能是△PAB的最大边,然后通过对应角相等.P只能是C点的对称点,且只有一点.
(2)把点A、B、C的坐标分别代入二次函数解析式,列出关于系数的方程组,通过解方程组来求系数的值.即利用待定系数法来求二次函数的解析式;
(3)两个三角形中的公共边是线段AB,且线段AB是抛物线以下△PAB中最大的一条边,那就说明AB边只能是△PAB的最大边,然后通过对应角相等.P只能是C点的对称点,且只有一点.
解答:解:(1)∵A(-1,0),B(2,0),
∴AB=3,
∵△ABC的面积为3,
∴
×3OC=3,即OC=2,
∴点C的坐标为(0,-2).
(2)∵A(-1,0),B(2,0),C(0,-2).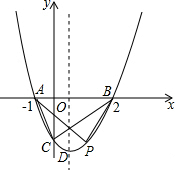
∴代入y=ax2+bx+c,得
,解得
,
∴抛物线的解析式为y=x2-x-2;
(3)设抛物线的顶点为D.
∵抛物线的解析式为y=x2-x-2=(x-
)2-
,
∴D(
,-
).
又A(-1,0),B(2,0),C(0,-2),
∴AB=3,AC=
,BC=2
,AD=BD=
,
∴在△ABC和△ABP中,都是线段AB最长,
∴以A,B,P为顶点的三角形与△ABC相似时,∠ACB=∠APB,
∴点C与点P关于x=
对称,
则P(1,-2).
∴AB=3,
∵△ABC的面积为3,
∴
| 1 |
| 2 |
∴点C的坐标为(0,-2).
(2)∵A(-1,0),B(2,0),C(0,-2).

∴代入y=ax2+bx+c,得
|
|
∴抛物线的解析式为y=x2-x-2;
(3)设抛物线的顶点为D.
∵抛物线的解析式为y=x2-x-2=(x-
| 1 |
| 2 |
| 9 |
| 4 |
∴D(
| 1 |
| 2 |
| 9 |
| 4 |
又A(-1,0),B(2,0),C(0,-2),
∴AB=3,AC=
| 5 |
| 2 |
3
| ||
| 4 |
∴在△ABC和△ABP中,都是线段AB最长,
∴以A,B,P为顶点的三角形与△ABC相似时,∠ACB=∠APB,
∴点C与点P关于x=
| 1 |
| 2 |
则P(1,-2).
点评:本题考查了二次函数综合题,其中涉及到了待定系数法求二次函数的解析式,二次函数图象上点的坐标特征以及相似三角形的判定与性质.以A,B,P为顶点的三角形与△ABP不是一个意思,不能混同.同时,本题涉及的抛物线是轴对称图形,务请注意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将点P(2,-3)绕原点旋转180度得到的点的坐标为( )
| A、(-2,-3) |
| B、(2,-3) |
| C、(-2,3) |
| D、(2,3) |
 一个长方形如图所示,恰分成6个正方形,其中最小的正方形的面积是1平方厘米,求正方形F的边长.
一个长方形如图所示,恰分成6个正方形,其中最小的正方形的面积是1平方厘米,求正方形F的边长. 如图,矩形ABCD中,AB=2,BC=2
如图,矩形ABCD中,AB=2,BC=2