题目内容
在直角坐标系中,⊙A和⊙B的圆心都在x轴上,且⊙A和⊙B的半径分别为3和2,已知点B的坐标为(3,0),点A(a,0),试讨论:当a取哪些值时,⊙A和⊙B分别外切、相交、内含和外离.
考点:圆与圆的位置关系,坐标与图形性质
专题:计算题
分析:根据圆和圆的位置关系,得到当AB=3+2时,⊙A和⊙B外切,即|a-3|=5;当3-2<AB<5时,⊙A和⊙B相交,即1<|a-3|<5;当0≤AB<3-2时,⊙A和⊙B内含,即0≤|a-3|<1;当AB>3+2时,⊙A和⊙B外离,即|a-3|>5,然后分别解方程或不等式得到对应的a的值或范围.
解答:解:当AB=3+2时,⊙A和⊙B外切,即|a-3|=5,解得a=-2或a=8;
当3-2<AB<5时,⊙A和⊙B相交,即1<|a-3|<5,解得-2<a<2或4<a<8;
当0≤AB<3-2时,⊙A和⊙B内含,即0≤|a-3|<1,解得2<a<4;
当AB>3+2时,⊙A和⊙B外离,即|a-3|>5,解得a<-2或a>8.
当3-2<AB<5时,⊙A和⊙B相交,即1<|a-3|<5,解得-2<a<2或4<a<8;
当0≤AB<3-2时,⊙A和⊙B内含,即0≤|a-3|<1,解得2<a<4;
当AB>3+2时,⊙A和⊙B外离,即|a-3|>5,解得a<-2或a>8.
点评:本题考查了圆和圆的位置关系:两圆的圆心距为d、两圆半径分别为R,r,若两圆外离?d>R+r;两圆外切?d=R+r;两圆相交?R-r<d<R+r(R≥r);两圆内切?d=R-r(R>r);两圆内含?d<R-r(R>r).也考查了坐标与图形性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,点D是△ABC的边CA延长线上的一定点,点E为AB上一动点,求证:无论点E怎样运动,都有∠DEB=∠B+∠C+∠D.
如图所示,点D是△ABC的边CA延长线上的一定点,点E为AB上一动点,求证:无论点E怎样运动,都有∠DEB=∠B+∠C+∠D.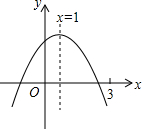 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①a+b=0;②a-b+c>0;③当m≠1时,a+b>am2+bm;④3a+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①a+b=0;②a-b+c>0;③当m≠1时,a+b>am2+bm;④3a+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有 在1998年特大洪水时期,要加固全长为10000m的河堤.大堤高5m,坝顶宽4m,迎水坡和背水坡都是坡度为1:1的等腰梯形.现要将大堤加高1m,背水坡坡度改为1:1.5.已知坝顶宽不变,求大坝横截面面积增加了多少平方米?完成工程需多少立方米的土石?
在1998年特大洪水时期,要加固全长为10000m的河堤.大堤高5m,坝顶宽4m,迎水坡和背水坡都是坡度为1:1的等腰梯形.现要将大堤加高1m,背水坡坡度改为1:1.5.已知坝顶宽不变,求大坝横截面面积增加了多少平方米?完成工程需多少立方米的土石?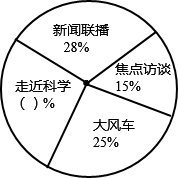 如图是某学校教师喜欢看的电视节目统计图.
如图是某学校教师喜欢看的电视节目统计图.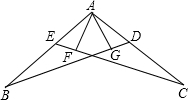 如图,AB=AC,AG⊥BD,AF⊥CE,AG=AF,求证:AD=AE.
如图,AB=AC,AG⊥BD,AF⊥CE,AG=AF,求证:AD=AE.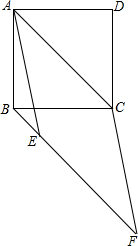 如图,已知AC是正方形ABCD的对角线,BE∥AC,点E在BF上,且AE=AC,CF∥AE,求∠BCF.
如图,已知AC是正方形ABCD的对角线,BE∥AC,点E在BF上,且AE=AC,CF∥AE,求∠BCF.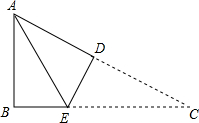 如图,在△ABC中,∠B=90°,∠C=30°,AB=3,BC=3
如图,在△ABC中,∠B=90°,∠C=30°,AB=3,BC=3