题目内容
19.已知在一个不透明的口袋中,有四个除颜色外均相同的球,其中1个白球,3个黑球.(1)从口袋中随机取出一个球(不放回),接着再取一个球,取出的两个球都是黑色的概率是多少?
(2)往该口袋中又放入白球和黑球若干,且一种球的个数比另一种球的个数多1,此时从口袋中取出一个黑球的概率为$\frac{2}{3}$,放入该口袋中白球和黑球各多少个?
分析 (1)利用独立事件同时发生的概率等于两个独立事件发生概率的积直接求解即可;
(2)设白球有x个,黑球(x+1)个,根据“从口袋中取出一个黑球的概率为$\frac{2}{3}$”列出方程求解即可.
解答 解:(1)∵第一次取球为黑色的概率为$\frac{3}{4}$,第二次取球为黑色的概率为$\frac{2}{3}$,
∴取出的两个球都是黑色的概率是$\frac{3}{4}$×$\frac{2}{3}$=$\frac{1}{2}$;
(2)设白球有x个,黑球(x+1)个,
则$\frac{x+1+3}{x+1+x+1+3}$=$\frac{2}{3}$,
解得:x=2,
∴放入白球2个,黑球3个.
点评 本题考查概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为( )
如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为( )
 如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为( )
如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
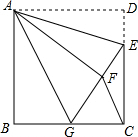 如图,正方形ABCD中,AB=6,点E在边CD上,且DE=2.将△ADE沿AE对折得到△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②AG∥CF;③sin∠EGC=$\frac{4}{5}$;④S△AGE=15.其中正确的结论是①②③④.(只填序号)
如图,正方形ABCD中,AB=6,点E在边CD上,且DE=2.将△ADE沿AE对折得到△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②AG∥CF;③sin∠EGC=$\frac{4}{5}$;④S△AGE=15.其中正确的结论是①②③④.(只填序号)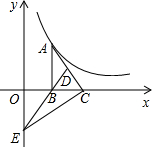 如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.