题目内容
 如图,将一块直角三角形纸板的直角顶点放在点C(1,
如图,将一块直角三角形纸板的直角顶点放在点C(1,| 1 |
| 2 |
| 9 |
| 2 |
| m |
| x |
(1)试用含有m或k的代数式表示点A和点B的坐标;
(2)求直线AB及双曲线的解析式;
(3)设双曲线y=
| m |
| x |
考点:反比例函数综合题,相似三角形的判定与性质
专题:综合题
分析:(1)由题可得xA=xC=1,yB=yC=
,然后只需代入直线或双曲线的解析式,就可解决问题;
(2)根据点A、点B坐标的两种表示建立关于k和m的方程组,然后只需解这个方程组就可解决问题;
(3)易证△ACB∽△MPN,根据相似三角形的性质可求出MP,设点P的横坐标为a,就可得到yM、yP(用a的代数式表示),根据MP=yM-yP建立关于a的方程,解这个方程就可解决问题.
| 1 |
| 2 |
(2)根据点A、点B坐标的两种表示建立关于k和m的方程组,然后只需解这个方程组就可解决问题;
(3)易证△ACB∽△MPN,根据相似三角形的性质可求出MP,设点P的横坐标为a,就可得到yM、yP(用a的代数式表示),根据MP=yM-yP建立关于a的方程,解这个方程就可解决问题.
解答:解:(1)由题可得:xA=xC=1,yB=yC=
.
∵点A、B在直线y=kx+
上,
∴yA=k+
,kxB+
=
即xB=-
,
∴点A为(1,k+
),点B为(-
,
).
∵点A、B在双曲线y=
(m>0)上,
∴yA=
=m,
=
即xB=2m,
∴点A为(1,m),点B为(2m,
).
∴点A的坐标可表示为(1,k+
),也可表示为(1,m),
点B的坐标可表示为(-
,
),也可表示为(2m,
).
(2)由(1)可得:
,
解得:
或
.
∵yA>yC,即m>
,
∴k=-
,m=4,
∴直线AB的解析式为y=-
x+
,双曲线的解析式为y=
;
(3)假设存在点P,使得△ABC的面积是△MNP面积的四倍.
∵MP∥AC∥y轴,PN∥BC∥x轴,
∴∠CAB=∠PMN,∠ABC=∠MNP,
∴△ACB∽△MPN,
∴
=(
)2=4,
∴AC=2MP.
∵AC=yA-yC=4-
=
,
∴MP=
.
设点P的横坐标为a,则点M的横坐标也为a,
∴yM=-
a+
,yN=
,
∴MP=yM-yP=-
a+
-
=
,
整理得:2a2-11a+16=0.
∵△=(-11)2-4×2×16=-7<0,
∴该方程无解,
所以假设不成立,
因此不存在点P,使得△ABC的面积是△MNP面积的四倍.
| 1 |
| 2 |
∵点A、B在直线y=kx+
| 9 |
| 2 |
∴yA=k+
| 9 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 4 |
| k |
∴点A为(1,k+
| 9 |
| 2 |
| 4 |
| k |
| 1 |
| 2 |
∵点A、B在双曲线y=
| m |
| x |
∴yA=
| m |
| 1 |
| m |
| xB |
| 1 |
| 2 |
∴点A为(1,m),点B为(2m,
| 1 |
| 2 |
∴点A的坐标可表示为(1,k+
| 9 |
| 2 |
点B的坐标可表示为(-
| 4 |
| k |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)可得:
|
解得:
|
|
∵yA>yC,即m>
| 1 |
| 2 |
∴k=-
| 1 |
| 2 |
∴直线AB的解析式为y=-
| 1 |
| 2 |
| 9 |
| 2 |
| 4 |
| x |

(3)假设存在点P,使得△ABC的面积是△MNP面积的四倍.
∵MP∥AC∥y轴,PN∥BC∥x轴,
∴∠CAB=∠PMN,∠ABC=∠MNP,
∴△ACB∽△MPN,
∴
| S△ACB |
| S△MPN |
| AC |
| MP |
∴AC=2MP.
∵AC=yA-yC=4-
| 1 |
| 2 |
| 7 |
| 2 |
∴MP=
| 7 |
| 4 |
设点P的横坐标为a,则点M的横坐标也为a,
∴yM=-
| 1 |
| 2 |
| 9 |
| 2 |
| 4 |
| a |
∴MP=yM-yP=-
| 1 |
| 2 |
| 9 |
| 2 |
| 4 |
| a |
| 7 |
| 4 |
整理得:2a2-11a+16=0.
∵△=(-11)2-4×2×16=-7<0,
∴该方程无解,
所以假设不成立,
因此不存在点P,使得△ABC的面积是△MNP面积的四倍.
点评:本题主要考查了用待定系数法求直线及双曲线的解析式、相似三角形的判定与性质、解方程组等知识,根据点A、点B坐标的两种表示方法建立方程组是解决第(2)小题的关键,利用MP=yM-yP建立方程是解决第(3)小题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,如果∠AGD=∠ACB,CD⊥AB,EF⊥AB,那么∠1=∠2吗?试说明理由.
如图,在△ABC中,如果∠AGD=∠ACB,CD⊥AB,EF⊥AB,那么∠1=∠2吗?试说明理由.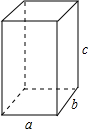 如图是一个体积为25cm3的长方体工件,其中a、b、c分别表示它的长、宽、高,且a:b:c=2:1:3,请你求出这个工件的表面积(精确到0.1cm2).
如图是一个体积为25cm3的长方体工件,其中a、b、c分别表示它的长、宽、高,且a:b:c=2:1:3,请你求出这个工件的表面积(精确到0.1cm2).