题目内容
7.△ABC是等边三角形,点D是射线上BC上的一个动点(点D不与点B,C重合,△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.如图1所示,当点D在线段BC上时.
(1)求证:△AEB≌△ADC;
(2)探究四边形BCGE是哪种特殊的四边形,并说明理由.如图2所示,当点D在BC的延长线上时,直接写出(1)中的结论是否成立.
分析 (1)根据等边三角形的性质得AB=AC,AE=AD,∠BAC=∠EAD=60°,利用等量减等量差相等可得到∠DAC=∠BAE,则可根据“SAS”证明△ABE≌△ADC;
(2)由△ABC和△DE都是等边三角形得到∠ACB=∠BAC=60°,由△ABE≌△ADC得到∠ABE=∠ACD=60°,则∠ABE=∠BAC,根据平行线的判定得到BE∥AC,加上EG∥BC,于是根据平行四边形的判定方法得到四边形BCGE为平行四边形;与(1)一样可证得△ABE≌△ADC.
解答 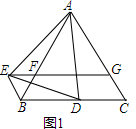 (1)证明:∵△ABC和△DE都是等边三角形,
(1)证明:∵△ABC和△DE都是等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∴∠BAC-∠BAD=∠EAD-∠BAD,即∠DAC=∠BAE,
在△ABE和△ADC中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠DAC}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ADC(SAS);
(2)四边形BCGE是平行四边形.
理由如下:
∵△ABC和△DE都是等边三角形,
∴∠ACB=∠BAC=60°,
∵△ABE≌△ADC,
∴∠ABE=∠ACD=60°,
∴∠ABE=∠BAC,
∴BE∥AC,
∵EG∥BC,
∴四边形BCGE为平行四边形;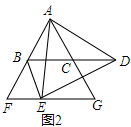
成立,理由如下:
∵△ABC和△DE都是等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∴∠BAC-∠EAG=∠EAD-∠EAG,即∠DAC=∠BAE,
在△ABE和△ADC中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠DAC}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ADC(SAS).
点评 本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的性质、平行四边形的判定和菱形的判定.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案| A. | 5 | B. | 12 | C. | 6 | D. | 10 |

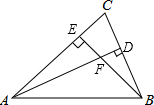 如图,已知△ABC的两条高AD、BE交于F,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:AF=BC.
如图,已知△ABC的两条高AD、BE交于F,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:AF=BC.