题目内容
15.已知二次函数y=(x+1)2-4.(1)指出函数图象的开口方向、对称轴和顶点坐标;
(2)若图象与x轴的交点为A,B,与y轴的交点为C,求S△ABC;
(3)指出该函数的最值和增减情况.
分析 (1)利用二次根式的性质确定出开口方向,顶点坐标以及对称轴即可,
(2)令y=0,得出x的值,得出A、B两点的坐标,令x=0得出点C的坐标,根据三角形的面积公式得出S△ABC;
(3)根据开口方向和顶点坐标得出最值,再由对称轴和开口方向得出增减性.
解答 解:(1)∵a=1>0,
∴抛物线开口向上,
顶点坐标为(-1,-4),对称轴为直线x=-1;
(2)令y=0,得0=(x+1)2-4,
解得x1=1,x2=-3,
∴A(1,0),B(-3,0),
令x=0,得y=-3,
∴C(0,-3),
∴S△ABC=$\frac{1}{2}$×4×3=6;
(3)∵-$\frac{b}{2a}$=-$\frac{2}{2×1}$=-1,
$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×1×(-3)-4}{4}$=-4,
∴当x<-1,y随x的增大而减小,当x>-1,y随x的增大而增大,函数有最小值-4.
点评 本题考查了抛物线和x轴的交点问题,由二次函数的性质求抛物线的对称轴和顶点坐标,最值,增减性是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
20.下列几对数中,互为相反数的是( )
| A. | $\frac{3}{4}$和-0.75 | B. | -5和﹢3 | C. | $\frac{1}{3}$和0.3 | D. | $\frac{1}{2}$和-2 |
5.数轴上的点A到表示-1的点B距离是6,则点A表示的数为( )
| A. | 6或-6 | B. | 5 | C. | -7 | D. | 5或-7 |


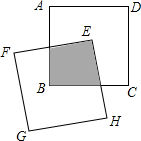 如图,两个边长为1的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E旋转,则它们重叠部分的面积为S=$\frac{1}{4}$.
如图,两个边长为1的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E旋转,则它们重叠部分的面积为S=$\frac{1}{4}$.