题目内容
17.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一条短边长为2,则另外一个三角形的周长为7.5.分析 由一个三角形的三边长是4、5、6,即可求得此三角形的周长,又由相似三角形周长的比等于相似比,即可求得另一个三角形的周长.
解答 解:设另外一个三角形的周长是x,
∵一个三角形的三边长是4、5、6,
∴这个三角形的周长为:4+5+6=15,
∵与它相似的另一个三角形最短的一边长是2,
∴$\frac{x}{15}$=$\frac{2}{4}$,
解得:x=7.5,
∴另一个三角形的周长是7.5.
故答案为7.5.
点评 此题考查了相似三角形的性质.解题的关键是注意掌握相似三角形周长的比等于相似比定理的应用.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
7.如果x2-6x+k是完全平方式,则k的值为( )
| A. | ±9 | B. | ±36 | C. | 36 | D. | 9 |
5.菱形ABCD的两条对角线长分别为10和24,求菱形的高( )
| A. | 120 | B. | 240 | C. | $\frac{60}{13}$ | D. | $\frac{120}{13}$ |
12.一个三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( )
| A. | 24cm | B. | 21cm | C. | 13cm | D. | 9cm |
2. 如图,若AB∥CD,CD∥EF,则AB与EF的位置关系是( )
如图,若AB∥CD,CD∥EF,则AB与EF的位置关系是( )
 如图,若AB∥CD,CD∥EF,则AB与EF的位置关系是( )
如图,若AB∥CD,CD∥EF,则AB与EF的位置关系是( )| A. | 平行 | B. | 延长后才平行 | C. | 垂直 | D. | 难以确定 |
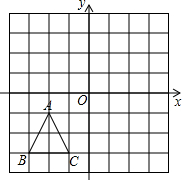 如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3)
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3) 如图,菱形ABCD的边长为1cm,∠BAD=120°,将菱形ABCD绕点B顺时针旋转a°(0°<a<180°),使BA与BC重合,则在旋转过程中,点D所走的路径$\widehat{DD′}$的长为$\frac{\sqrt{3}}{3}π$cm(结果不取近似值)
如图,菱形ABCD的边长为1cm,∠BAD=120°,将菱形ABCD绕点B顺时针旋转a°(0°<a<180°),使BA与BC重合,则在旋转过程中,点D所走的路径$\widehat{DD′}$的长为$\frac{\sqrt{3}}{3}π$cm(结果不取近似值)