题目内容
20.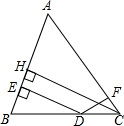 如图,已知△ABC是等腰三角形,AB=AC,D是BC边上的任意一点,且DE⊥AB,DF⊥AC,CH⊥AB,垂足分别为E,F,H,求证:DE+DF=CH.
如图,已知△ABC是等腰三角形,AB=AC,D是BC边上的任意一点,且DE⊥AB,DF⊥AC,CH⊥AB,垂足分别为E,F,H,求证:DE+DF=CH.
分析 连接AD,利用等积法可得到AB•DE+AC•DF=AB•CH,可证得结论.
解答 证明:
如图,连接AD,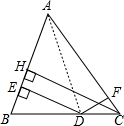
∵DE⊥AB,DF⊥AC,CH⊥AB,
∴S△ABD=$\frac{1}{2}$AB•DE,S△ACD=$\frac{1}{2}$AC•DF,S△ABC=$\frac{1}{2}$AB•CH,
∵S△ABD+S△ACD=S△ABC,
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$AB•CH,
∵AB=AC,
∴DE+DF=CH.
点评 本题主要考查等积法的应用,掌握等积法是解题的关键,即从不同的角度表示同一个图形的面积,从而可得到有关线段之间的关系.

练习册系列答案
相关题目
11. 如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )
如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )
 如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )
如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )| A. | 主视图 | B. | 俯视图 | C. | 左视图 | D. | 三视图 |
8.在△ABC中,BC边上的高AH一定满足( )
| A. | 在△ABC的内部 | B. | AH≤AB | C. | AH≤BH | D. | ∠AHC=90° |
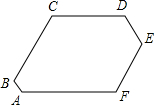 如图,已知六边形ABCDEF的每个内角都是120°且AB=1,DE=2,BC=CD=8,求此六边形的周长.
如图,已知六边形ABCDEF的每个内角都是120°且AB=1,DE=2,BC=CD=8,求此六边形的周长.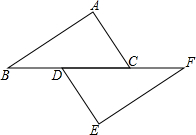 △ABC和△FED中,BD=FC,∠B=∠F.当添加条件AB=EF时,就可得到△ABC≌△FED,依据是SAS(只需填写一个你认为正确的条件).
△ABC和△FED中,BD=FC,∠B=∠F.当添加条件AB=EF时,就可得到△ABC≌△FED,依据是SAS(只需填写一个你认为正确的条件).