题目内容
4.观察下列等式:第一个等式:a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$
第二个等式:a2=$\frac{4}{2×3×{2}^{2}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$
第三个等式:a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$
第四个等式:a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$
按上述规律,回答以下问题:
(1)用含n的代数式表示第n个等式:an=$\frac{n+2}{n(n+1)×{2}^{n+1}}$=$\frac{1}{n×{2}^{n}}$-$\frac{1}{(n+1)×{2}^{n+1}}$.
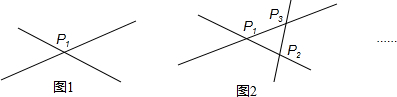
(2)当平面内共有两条直线相交时,能找到一个交点P1(如图1),当图中有三条直线两两相交时,最多能找到三个交点P1、P2、P3(如图2),试回答下列问题:
①当图中有4条直线两两相交时,最多能找到几个交点?并用铅笔和直尺画出相应的图形.
②当图中有100条直线两两相交时,最多能找到多少个交点?(请列出算式,并求出结果)
分析 (1)利用已知的等式类比得出an=$\frac{n+2}{n(n+1)×{2}^{n+1}}$=$\frac{1}{n×{2}^{n}}$-$\frac{1}{(n+1)×{2}^{n+1}}$;
(2)①4条直线两两相交,最多有1+2+3=6个交点;
②n条直线两两相交,最多有1+2+3+…+n-1=$\frac{1}{2}$n(n-1)个交点;由此代入求得答案即可.
解答 解:(1)an=$\frac{n+2}{n(n+1)×{2}^{n+1}}$=$\frac{1}{n×{2}^{n}}$-$\frac{1}{(n+1)×{2}^{n+1}}$;
(2)①4条直线两两相交,最多有6个交点;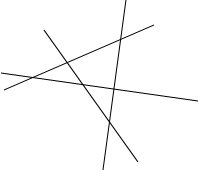
②1+2+3+…+99=$\frac{1}{2}$×99×(99+1)=4950.
答:100条直线两两相交时,最多能找到4950个交点.
点评 本题考查了图形的变化规律,是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律解决问题.

练习册系列答案
相关题目
16.解不等式组$\left\{\begin{array}{l}{2x+3≥x+4}\\{\frac{5x+2}{2}+1≥4x-1}\end{array}\right.$,并把解集在数轴上表示出来.
13.点P(3,-5)所在的象限是第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
14.如果点P位于x轴下方、y轴右侧,距离x轴5个单位长度,距离y轴3个单位长度,那么点P的坐标为( )
| A. | (5,-3) | B. | (3,-5) | C. | (-5,3) | D. | (-3,5) |
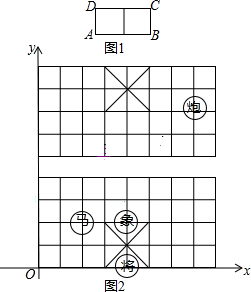 中国象棋中历来有“马”走“日”,“象”飞“田”之说,其意思是:在象棋棋盘上,“马”的走法如下:以“马”所在的位置为棋格所组成的任一“日”字的一个顶点,下一步“马”可以走到该“日”字与原位置相对的那个顶点,如图1马可以自A走到C(或自C走到A)也可自B走到D(或D走到B),在如图棋盘中,建立如图2所示直角坐标系:
中国象棋中历来有“马”走“日”,“象”飞“田”之说,其意思是:在象棋棋盘上,“马”的走法如下:以“马”所在的位置为棋格所组成的任一“日”字的一个顶点,下一步“马”可以走到该“日”字与原位置相对的那个顶点,如图1马可以自A走到C(或自C走到A)也可自B走到D(或D走到B),在如图棋盘中,建立如图2所示直角坐标系: 如图,在直径为12的半圆中,点C、D为半圆的三等分点,求图中阴影部分的面积.
如图,在直径为12的半圆中,点C、D为半圆的三等分点,求图中阴影部分的面积.