题目内容
某种产片的原料提价,因而厂家决定对于产品进行提价,现有三种方案:
(1)第一次提价p%,第二次提价q%;
(2)第一次提价q%,第二次提价p%;
(3)第一、二次提价均为
%.
其中p,q是不相等的正数,三种方案哪种提价最多?
(提示:因为p≠q,(p-q)2=p2-2pq+q2>0,所以p2+q2>2pq)
(1)第一次提价p%,第二次提价q%;
(2)第一次提价q%,第二次提价p%;
(3)第一、二次提价均为
| p+q |
| 2 |
其中p,q是不相等的正数,三种方案哪种提价最多?
(提示:因为p≠q,(p-q)2=p2-2pq+q2>0,所以p2+q2>2pq)
考点:列代数式
专题:
分析:根据各方案中的提价百分率,分别表示出提价后的单价,得到方案1:a(1+p)(1+q);方案2:a(1+q)(1+p);方案3:a(1+
)2,方案1和2显然相同,用方案3的单价减去方案1的单价,提取a,利用完全平方公式及多项式乘以多项式的法则化简,去括号合并后再利用完全平方公式变形,根据p不等于q判定出其差为正数,可得出a(1+
)2>a(1+p)(1+q),进而确定出方案3的提价多.
| p+q |
| 2 |
| p+q |
| 2 |
解答:解:方案1:a(1+p)(1+q);方案2:a(1+q)(1+p);方案3:a(1+
)2,
显然方案1、2结果相同,
a(1+
)2-a(1+p)(1+q)
=a[1+p+q+(
)2-(1+p+q+pq)]
=a(1+p+q+
-1-p-q-pq)
=a(
-pq)
=a•
=a•
,
∵p≠q,
∴
>0,
∴a•
>0,
∴a(1+
)2>a(1+p)(1+q),
∴提价最多的是方案3.
| p+q |
| 2 |
显然方案1、2结果相同,
a(1+
| p+q |
| 2 |
=a[1+p+q+(
| p+q |
| 2 |
=a(1+p+q+
| p2+2pq+q2 |
| 4 |
=a(
| p2+2pq+q2 |
| 4 |
=a•
| p2-2pq+q2 |
| 4 |
=a•
| (p-q)2 |
| 4 |
∵p≠q,
∴
| (p-q)2 |
| 4 |
∴a•
| (p-q)2 |
| 4 |
∴a(1+
| p+q |
| 2 |
∴提价最多的是方案3.
点评:此题考查了列代数式、整式混合运算的应用,利用的方法为作差法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
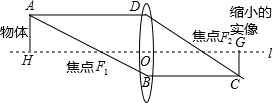 凸透镜成像的原理如图所示,AD∥l∥BC,若物体到焦点的距离与焦点到凸透镜的中心线DB的距离之比为5:4,则物体被缩小到原来的几分之几?
凸透镜成像的原理如图所示,AD∥l∥BC,若物体到焦点的距离与焦点到凸透镜的中心线DB的距离之比为5:4,则物体被缩小到原来的几分之几?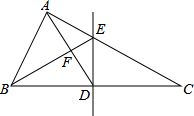 如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.