题目内容
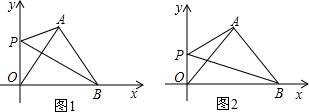
如图1,A是OB的垂直平分线上一点,P为y轴上一点且∠OPB=∠OAB.
(1)若∠AOB=60°,PB=4,求点P的坐标;
(2)在(1)的条件下,求证:PA+PO=PB;
(3)如图2,若点A是OB的垂直平分线上一点,已知A(2,5),∠OPB=∠OAB,求PO+PB的值.
(1)若∠AOB=60°,PB=4,求点P的坐标;
(2)在(1)的条件下,求证:PA+PO=PB;
(3)如图2,若点A是OB的垂直平分线上一点,已知A(2,5),∠OPB=∠OAB,求PO+PB的值.

考点:全等三角形的判定与性质,坐标与图形性质,线段垂直平分线的性质
专题:
分析:(1)根据垂直平分线性质可得OA=AB,根据∠AOB的大小可以求得∠OPB=60°,根据30°角所对直角边为斜边一半即可求得P点坐标;
(2)在PB上取一点E,使OP=OE,可证∠POA=∠EOB,可证△POA≌△EOB,可得PA=EB,即可解题;
(3)延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴,可证BP=PD,即可求得PO+PB=OP+PD=OD即可解题.
(2)在PB上取一点E,使OP=OE,可证∠POA=∠EOB,可证△POA≌△EOB,可得PA=EB,即可解题;
(3)延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴,可证BP=PD,即可求得PO+PB=OP+PD=OD即可解题.
解答:解:(1)∵∠OPB=∠OAB,∠AOB=60°,
∴∠OPB=60°,
∴∠OBP=30°,
∵PB=4,
∴OP=2,
∴P点坐标为(0,2);
(2)在PB上取一点E,使OP=OE,
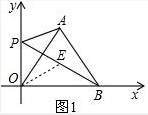
∵∠OPE=60°,
∴△POE是等边三角形,
∴∠POE=60°,PE=PO=OE,
∵∠AOB=60°,
∴∠POA=∠EOB
在△POA和△EOB中,
,
∴△POA≌△EOB(SAS),
∴PA=EB,
∴PB=PE+EB=PO+PA;
(3)延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴;
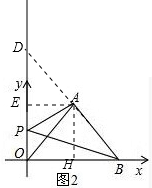
∵OA=AB,
∴∠AOB=∠ABO,
∵∠ABO+∠ODB=∠AOB+∠AOD=90°,
∴∠AOD=∠ODB,
∴∠ODB=∠ABP,
∴AD=OA,BP=PD,
∴E为OD中点,
∵OE=AH=5,
∴PO+PB=OP+PH+HB=OP+PE+OE=2OE=10.
∴∠OPB=60°,
∴∠OBP=30°,
∵PB=4,
∴OP=2,
∴P点坐标为(0,2);
(2)在PB上取一点E,使OP=OE,

∵∠OPE=60°,
∴△POE是等边三角形,
∴∠POE=60°,PE=PO=OE,
∵∠AOB=60°,
∴∠POA=∠EOB
在△POA和△EOB中,
|
∴△POA≌△EOB(SAS),
∴PA=EB,
∴PB=PE+EB=PO+PA;
(3)延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴;

∵OA=AB,
∴∠AOB=∠ABO,
∵∠ABO+∠ODB=∠AOB+∠AOD=90°,
∴∠AOD=∠ODB,
∴∠ODB=∠ABP,
∴AD=OA,BP=PD,
∴E为OD中点,
∵OE=AH=5,
∴PO+PB=OP+PH+HB=OP+PE+OE=2OE=10.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中每一问作辅助线构建全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知△ABC中,CA=CB,点O为AB的中点,∠ACB=120°,EF分别在直线AC、BC上,且∠EOF=60°.
已知△ABC中,CA=CB,点O为AB的中点,∠ACB=120°,EF分别在直线AC、BC上,且∠EOF=60°. 如图,△ABC是等腰三角形,D是底边BC上任意一点,DE⊥AB于点E,DF⊥AC于点F,若AB边上的高是6,求DE+DF的值.
如图,△ABC是等腰三角形,D是底边BC上任意一点,DE⊥AB于点E,DF⊥AC于点F,若AB边上的高是6,求DE+DF的值.