题目内容
16．某商店购进一批单价为18元的商品，试销中发现这批商品的日销售量m（件）是销售单价x（元）的一次函数：m=300-10x，请根据上述信息，说明商店将售价定为多少元时，可获得最大日销售利润．最大日销售利润是多少元？分析 根据总利润=单位利润×销售量列出函数关系式，然后将求得的函数关系式配方后即可确定其最值．
解答 解：设：最大日销售利润是y元，
由题意得：每件商品的销售利润为（x-18）元，
那么m件的销售利润为
y=m（x-18）=（300-10x）（x-18），
即y=-10x2+480x-5400=-10（（x-24）2+3600，
∴当x=24时，y有最大值，最大值y=3600，
∴当每件商品的销售价定为24元时，最大日销售利润是3600元．
点评 本题考查了二次函数的应用，解题的关键是从实际问题中整理出二次函数模型，并运用二次函数的知识解决实际问题．
练习册系列答案
相关题目
6．下列从左到右的变形，是分解因式的是（ ）
| A． | xy2（x-1）=x2y2-xy2 | B． | x2+x-5=（x-2）（x+3）+1 | C． | （a+3）（a-3）=a2-9 | D． | 2a2+4a=2a（a+2） |
所给的数轴上表示下列四个数，并把这四个数按从小到大的顺序，用“＜”号连接起来．
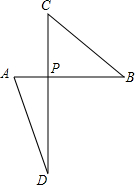如图，点P是线段AB的黄金分割点，将线段PB绕着点P逆时针旋转90°到点C，延长CP到点D．使PD=AB．连接AD，试比较△PCB与△PAD的面积大小，并说明理由．
如图，DE∥AC，CD平分∠ACB，EF平分∠BED．