题目内容
1.已知代数式A=2x2-3xy+4,B=$\frac{1}{2}$x2+xy-3,若C=A-2B,求代数式C.分析 将A、B代入C=A-2B,然后去括号、合并同类项即可求解.
解答 解:∵A=2x2-3xy+4,B=$\frac{1}{2}$x2+xy-3,
∴C=A-2B
=(2x2-3xy+4)-2($\frac{1}{2}$x2+xy-3)
=2x2-3xy+4-x2-2xy+6
=x2-5xy+10.
点评 本题考查了整式的加减,解答本题的关键是掌握去括号法则和合并同类项法则.

练习册系列答案
相关题目
11.若$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$,则$\frac{a+b}{b+c}$的值为( )
| A. | $\frac{7}{9}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{8}{7}$ |
6.下列从左到右的变形,是分解因式的是( )
| A. | xy2(x-1)=x2y2-xy2 | B. | x2+x-5=(x-2)(x+3)+1 | C. | (a+3)(a-3)=a2-9 | D. | 2a2+4a=2a(a+2) |
10.在数7,0,-(-3),π中,正数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
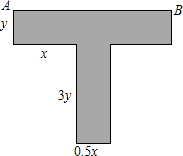 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求: 如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.
如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.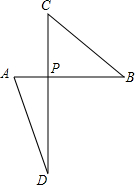 如图,点P是线段AB的黄金分割点,将线段PB绕着点P逆时针旋转90°到点C,延长CP到点D.使PD=AB.连接AD,试比较△PCB与△PAD的面积大小,并说明理由.
如图,点P是线段AB的黄金分割点,将线段PB绕着点P逆时针旋转90°到点C,延长CP到点D.使PD=AB.连接AD,试比较△PCB与△PAD的面积大小,并说明理由.