题目内容
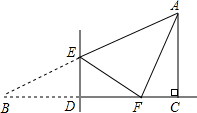 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=9.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=9.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为考点:翻折变换(折叠问题)
专题:
分析:首先由在Rt△ABC中,∠ACB=90°,∠B=30°,BC=9,即可求得AC的长、∠AEF与∠BAC的度数,然后分别从从∠AFE=90°与∠EAF=90°去分析求解,又由折叠的性质与三角函数的知识,即可求得CF的长,继而求得答案.
解答: 解:根据题意得:∠EFB=∠B=30°,DF=BD,EF=EB,
解:根据题意得:∠EFB=∠B=30°,DF=BD,EF=EB,
∵DE⊥BC,
∴∠FED=90°-∠EFD=60°,∠BEF=2∠FED=120°,
∴∠AEF=180°-∠BEF=60°,
∵在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,
∴AC=BC•tan∠B=9×
=3
,∠BAC=60°,
如图①若∠AFE=90°,
∵在Rt△ABC中,∠ACB=90°,
∴∠EFD+∠AFC=∠FAC+∠AFC=90°,
∴∠FAC=∠EFD=30°,
∴CF=AC•tan∠FAC=3
×
=3,
∴BD=DF=
=3;
如图②若∠EAF=90°,
则∠FAC=90°-∠BAC=30°,
∴CF=AC•tan∠FAC=3
×
=3,
∴BD=DF=
=6,
∴△AEF为直角三角形时,BD的长为:3或6.
故答案为:3或6.
 解:根据题意得:∠EFB=∠B=30°,DF=BD,EF=EB,
解:根据题意得:∠EFB=∠B=30°,DF=BD,EF=EB,∵DE⊥BC,
∴∠FED=90°-∠EFD=60°,∠BEF=2∠FED=120°,
∴∠AEF=180°-∠BEF=60°,
∵在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,
∴AC=BC•tan∠B=9×
| ||
| 3 |
| 3 |
如图①若∠AFE=90°,
∵在Rt△ABC中,∠ACB=90°,
∴∠EFD+∠AFC=∠FAC+∠AFC=90°,
∴∠FAC=∠EFD=30°,
∴CF=AC•tan∠FAC=3
| 3 |
| ||
| 3 |
∴BD=DF=
| BC-CF |
| 2 |
如图②若∠EAF=90°,
则∠FAC=90°-∠BAC=30°,
∴CF=AC•tan∠FAC=3
| 3 |
| ||
| 3 |
∴BD=DF=
| BC+CF |
| 2 |
∴△AEF为直角三角形时,BD的长为:3或6.
故答案为:3或6.
点评:此题考查了直角三角形的性质、折叠的性质以及特殊角的三角函数问题.此题难度适中,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
已知x=2,y=-4时,ax3+
by+5的值为2013,则当x=-4,y=-
时,代数式3ax-24by3+4242的值为( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、1231 | B、1230 |
| C、2230 | D、1234 |
 二次函数y=
二次函数y= 为了解中学生获取资讯的主要渠道,为了解中学生获取资讯的主要渠道,设置“A.报纸,B.电视,C.网络,D.身边的人,E.其他”五个选项(五项中必选且只能选一项)的调查问卷.先随机抽取50名中学生进行该问卷调查.根据调查的结果绘制条形图如图.该调查的方式是
为了解中学生获取资讯的主要渠道,为了解中学生获取资讯的主要渠道,设置“A.报纸,B.电视,C.网络,D.身边的人,E.其他”五个选项(五项中必选且只能选一项)的调查问卷.先随机抽取50名中学生进行该问卷调查.根据调查的结果绘制条形图如图.该调查的方式是